
 |
|||||
 |
|||||
Next: Results Up: Registration Algorithm Previous: Transformation Parameterization
Estimation Procedure
The Fourier series parameterization in Eq. 6
is a multi-resolution decomposition of the displacement fields. Let
![]() represent a family of subsets
of
represent a family of subsets
of ![]() where
where
![]() and the set subtraction
notation
and the set subtraction
notation
![]() is defined as all elements of A not in B. Figure 2
illustrates the definition of
is defined as all elements of A not in B. Figure 2
illustrates the definition of
![]() using a 2D example. In practice, the low frequency basis
coefficients are estimated before the higher ones allowing the global
image features to be registered before the local features. This is accomplished
by replacing Eq. 7
by
using a 2D example. In practice, the low frequency basis
coefficients are estimated before the higher ones allowing the global
image features to be registered before the local features. This is accomplished
by replacing Eq. 7
by
where
The image registration problem can be stated mathematically by combining
Eqs. (2), (3),
(4), and (9)
and estimating the set of parameters
![]() that minimize the combined cost function
that minimize the combined cost function
The constants
The basis coefficients
![]() are determined
by gradient descent using
are determined
by gradient descent using
where
![$\displaystyle \frac {\partial C(\mu,\eta)}{\partial a[k]} = Re\{ I_0[k] + I_2[k]\}, \quad \frac {\partial C(\mu,\eta)}{\partial b[k]} = Im\{-I_0[k] + I_2[k]\},$](img190.png) |
|
![$\displaystyle \frac {\partial C(\mu,\eta)}{\partial c[k]} = Re\{ I_1[k] + I_3[k]\}, \quad \frac {\partial C(\mu,\eta)}{\partial d[k]} = Im\{-I_1[k] + I_3[k]\}$](img191.png) |
where
![$\displaystyle = \frac 4 {N_1 N_2 N_3} \sum_{n \in \Omega_d} \Big( \sigma \big( ...
...h_d[n,r]} + \chi\big(u_d[n,r] - \tilde{w}_d[n,r] \big) \Big) e^{j<x,\theta[k]>}$](img193.png) |
||
![$\displaystyle = \frac 4 {N_1 N_2 N_3} \sum_{n \in \Omega_d} \Big( \sigma \big( ...
...g_d[n,r]} + \chi\big(w_d[n,r] - \tilde{u}_d[n,r] \big) \Big) e^{j<x,\theta[k]>}$](img195.png) |
||
The terms
The steps involved in estimating the basis coefficients ![]() and
and ![]() are summarized in the following algorithm.
are summarized in the following algorithm.
Algorithm
- Set
![$ \mu[k] = \eta[k] = 0$](img209.png) for
for
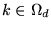 and set
and set
![$ r = [1, 1, 1]^T$](img210.png) .
. - Compute
![$ g_d^{-1}[n,r]$](img211.png) using the procedure described in Section 2.3
and set
using the procedure described in Section 2.3
and set
![$ \tilde{w}_d[n,r] = g_d^{-1}[n,r] - \frac n N$](img212.png) .
. - Compute new forward basis coefficients
![$ \mu[k] = a[k] + jb[k]$](img133.png) using Eq. 13.
using Eq. 13.
- Compute the forward displacement field
![$ u_d[n,r]$](img213.png) using Eq. 11.
using Eq. 11. - Compute
![$ h_d^{-1}[n,r]$](img214.png) using the procedure described in Section 2.3
and set
using the procedure described in Section 2.3
and set
![$ \tilde{u}_d [n,r] = h_d^{-1}[n,r] - \frac n N$](img215.png) .
. - Compute new reverse basis coefficients
![$ \eta[k] = c[k] + j d[k]$](img216.png) using Eq. 14.
using Eq. 14.
- Compute the reverse displacement field
![$ w_d[n,r]$](img217.png) using Eq. 11.
using Eq. 11. - If the criteria is met to increase the number of basis functions then
set
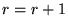 , and set the new coefficients in Eq. 11
to zero.
, and set the new coefficients in Eq. 11
to zero. - If the algorithm has not converged or reached the maximum number of iterations goto step 2.
- Use forward displacement field
![$ u_d[n]$](img219.png) to transform the template image
to transform the template image ![$ T_d[n]$](img33.png) and reverse displacement field
and reverse displacement field ![$ w_d[n]$](img220.png) to transform the target image
to transform the target image ![$ S_d[n]$](img221.png) .
.
Next: Results Up: Registration Algorithm Previous: Transformation Parameterization Xiujuan Geng 2002-07-04
Copyright © 2002 • The University of Iowa. All rights reserved.
Iowa City, Iowa 52242
Questions or Comments: gary-christensen@uiowa.edu
![$\displaystyle u_d [n,r] = \sum_{k \in \Omega_d[r]} \mu[k] e^{j<n,\theta[k]>}$](img155.png) and
and![$\displaystyle \quad w_d [n,r] = \sum_{k \in \Omega_d[r]} \eta[k] e^{j<n,\theta[k]>} .$](img156.png)
![\begin{multline}
C(\mu,\eta,r) =
\sigma \frac 1 {N_1 N_2 N_3} \sum_{n \in \Ome...
...\mu^{\dag }[k] D^2 [k] \mu [k]
+ \eta^{\dag }[k] D^2[k] \eta[k].
\end{multline}](img173.png)
![$\displaystyle a^{(n+1)}[k] = a^{(n)}[k] + \varepsilon \frac {\partial C(\mu^{(n...
...(n)}[k] + \varepsilon \frac {\partial C(\mu^{(n)},\eta^{(n)})}{\partial b[k]} ,$](img176.png)
![$\displaystyle c^{(n+1)}[k] = c^{(n)}[k] + \varepsilon \frac {\partial C(\mu^{(n...
...^{(n)}[k] + \varepsilon \frac {\partial C(\mu^{(n)},\eta^{(n)})}{\partial d[k]}$](img177.png)