
 |
|||||
 |
|||||
Next: Inverse Consistency Constraint Up: Registration Algorithm Previous: Problem Statement
Symmetric Similarity Cost Function
The problem with many image registration techniques is that the image similarity function does not uniquely determine the correspondence between two image volumes. In general, similarity cost functions have many local minima due to the complexity of the images being matched and the dimensionality of the transformation. It is these local minima (ambiguities) that cause the estimated transformation from image T to S to be different from the inverse of the estimated transformation from S to T. In general, this becomes more of a problem as the dimensionality of the transformation increases.
To overcome correspondence ambiguities, the transformations from image
![]() to
to ![]() and from
and from ![]() to
to ![]() are jointly estimated. This is accomplished by defining a cost function
to measure the shape differences between the deformed image
are jointly estimated. This is accomplished by defining a cost function
to measure the shape differences between the deformed image ![]() and image
and image ![]() and the differences between the deformed image
and the differences between the deformed image ![]() and image
and image ![]() . Ideally, the transformations
. Ideally, the transformations ![]() and
and ![]() should be inverses of one another, i.e.,
should be inverses of one another, i.e.,
![]() . In this work, the transformations
. In this work, the transformations ![]() and
and ![]() are estimated by minimizing a cost function
are estimated by minimizing a cost function
where the intensities of
In practice, the images ![]() and
and ![]() are discrete and the integrals in Eq. 1
are discretized and implemented as summations:
are discrete and the integrals in Eq. 1
are discretized and implemented as summations:
where the notation
Note that this joint estimation approach applies to both linear and non-linear transformations. In general, the squared-error similarity functions in Eq. 1 can be replaced by any suitable similarity function--mutual information [25,26], demons [6], an intensity variance cost function [27], etc.--where the choice is dependent on the particular registration application (see Discussion).
Next: Inverse Consistency Constraint Up: Registration Algorithm Previous: Problem Statement Xiujuan Geng 2002-07-04
Copyright © 2002 • The University of Iowa. All rights reserved.
Iowa City, Iowa 52242
Questions or Comments: gary-christensen@uiowa.edu
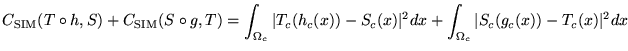
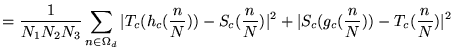
![$\displaystyle = \frac 1 {N_1 N_2 N_3} \sum_{n \in \Omega_d} \vert T_c(h_d[n]) - S_d[n]\vert^2 + \vert S_c(g_d[n]) - T_d[n]\vert^2$](img69.png)
![$\displaystyle = \frac 1 {N_1 N_2 N_3} \sum_{n \in \Omega_d} \vert T_d[N h_d[n]] - S_d[n]\vert^2 + \vert S_d[N g_d[n]] - T_d[n]\vert^2$](img70.png)