
 |
|||||
 |
|||||
- ... symmetry1
- This proposition assumes that
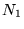 is even. A similar statement can be made when
is even. A similar statement can be made when 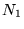 is odd.
is odd.
- ... discretizing2
- Symmetric difference equations were used to discretize the continuous
derivatives. For example, let
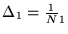 and
and
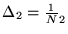 and then
and then
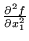 was replaced by
was replaced by
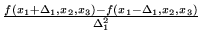 and
and
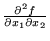 was replaced by
was replaced by
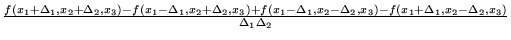 .
.
- ... equation3
- The notation
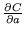 where
where  is a scalar-valued function and
is a scalar-valued function and  is a
is a
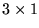 vector is defined as the
vector is defined as the
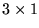 vector
vector
![$ [\frac {\partial C}{\partial a_1}, \frac {\partial C}{\partial a_2},
\frac {\partial C}{\partial a_3}]^T$](img183.png) .
.
- ... derivatives4
- The coefficients
![$ \tilde{\mu}[k]$](img187.png) and
and
![$ \tilde{\eta}[k]$](img188.png) are assumed to be constant when computing the partial
derivatives.
are assumed to be constant when computing the partial
derivatives.
- ... equations5
- The gradient of
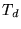 evaluated at
evaluated at  is computed as
is computed as
![$ [\frac {N_1}{2}(T_d[n_1+1,n_2,n_3] - T_d[n_1-1,n_2,n_3]),
\frac {N_2}{2}(T_d[...
..._d[n_1,n_2-1,n_3]),
\frac {N_3}{2}(T_d[n_1,n_2,n_3+1] - T_d[n_1,n_2,n_3-1])]^T$](img207.png)
- ... units6
- The minimum was computed as
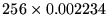 and the maximum as
and the maximum as
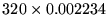 .
.
- ... units7
- The minimum was computed as
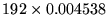 and the maximum as
and the maximum as
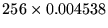 .
.
Copyright © 2002 • The University of Iowa. All rights reserved.
Iowa City, Iowa 52242
Questions or Comments: gary-christensen@uiowa.edu