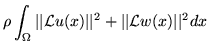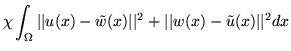|
|||||
 |
|||||
Next: Consistent Intensity-based Registration Up: Methods Previous: Unidirectional Landmark Thin-Plate Spline
Consistent Landmark Thin-Plate Spline Registration
The averaged unidirectional landmark-based thin-plate spline (AUL-TPS) image registration algorithm produces consistent correspondence only at the landmark locations. The consistent landmark-based, thin-plate spline (CL-TPS) image registration algorithm is designed to align the landmark points and minimize the consistency errors across the entire image domain.
The CL-TPS algorithm is solved by minimizing the cost function given
by
The first integral of the cost function defines the bending energy of the thin-plate spline for the displacement fields
Equation 4 is minimized numerically
using the CL-TPS algorithm described in Figure 3.
The algorithm is initialized with the forward and reverse displacement
fields ![]() and
and ![]() either set to zero as in Figure 3
or with the result of a previous registration algorithm. The temporary
variables
either set to zero as in Figure 3
or with the result of a previous registration algorithm. The temporary
variables ![]() and
and ![]() are initially set equal to the landmark locations
are initially set equal to the landmark locations ![]() and
and ![]() , respectively, for
, respectively, for
![]() . The value of
. The value of ![]() converges from
converges from ![]() to
to ![]() as the algorithm converges, and in similar fashion, the value of
as the algorithm converges, and in similar fashion, the value of
![]() converges from
converges from ![]() to
to ![]() .
.
|
At each iteration of the algorithm, the unidirectional landmark thin-plate
spline (UL-TPS) algorithm with periodic boundary conditions is used to
solve for the perturbation field ![]() that minimizes the distance between the current position of
that minimizes the distance between the current position of ![]() and its final position
and its final position ![]() . The perturbation field
. The perturbation field ![]() times the step size
times the step size ![]() is added to the current estimate of the forward displacement
field
is added to the current estimate of the forward displacement
field ![]() where
where ![]() is a positive number less than one. This procedure is repeated
to update the reverse displacement field
is a positive number less than one. This procedure is repeated
to update the reverse displacement field ![]() . Next, the forward displacement field
. Next, the forward displacement field ![]() is updated with the step size
is updated with the step size ![]() times the gradient of the inverse consistency constraint with
respect to
times the gradient of the inverse consistency constraint with
respect to ![]() assuming that
assuming that ![]() is constant. The displacement field
is constant. The displacement field ![]() is computed by taking the inverse of the transformation
is computed by taking the inverse of the transformation
![]() as described in our previous paper describing the consistent
intensity registration algorithm [34]. This step is repeated in the
reverse direction to update the displacement field
as described in our previous paper describing the consistent
intensity registration algorithm [34]. This step is repeated in the
reverse direction to update the displacement field ![]() . These steps are repeated until the landmark error and the inverse
consistency error fall below problem specific thresholds or until a specified
number of iterations are reached. In practice, this algorithm converges
to an acceptable solution within five to ten iterations and therefore
we use a maximum number of iterations as our stopping criteria.
. These steps are repeated until the landmark error and the inverse
consistency error fall below problem specific thresholds or until a specified
number of iterations are reached. In practice, this algorithm converges
to an acceptable solution within five to ten iterations and therefore
we use a maximum number of iterations as our stopping criteria.
Next: Consistent Intensity-based Registration Up: Methods Previous: Unidirectional Landmark Thin-Plate Spline Xiujuan Geng 2002-07-04
Copyright © 2002 • The University of Iowa. All rights reserved.
Iowa City, Iowa 52242
Questions or Comments: gary-christensen@uiowa.edu