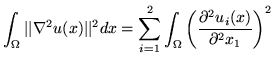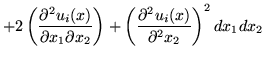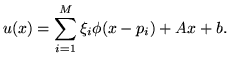Unidirectional Landmark Thin-Plate Spline Registration

The unidirectional landmark-based, thin-plate spline (UL-TPS) image registration algorithm [1,2,23] registers a template image $T(x)$ with a target image $S(x)$ by matching corresponding landmarks identified in both images. Registration at non-landmark points is accomplished by interpolation such that the overall transformation smoothly maps the template into the shape of the target image.

The unidirectional landmark image registration problem can be thought of as a Dirichlet problem [25] and can be stated mathematically as finding the displacement field $u$ that minimizes the cost function

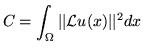$$C = \int_{\Omega} \vert\vert{\mathcal L}u(x)\vert\vert^2 dx$$ (1)

subject to the constraints that $u(p_i) = q_i - p_i$ for $i = 1, \ldots, M$. The operator ${\mathcal L}$ denotes a symmetric linear differential operator [36] and is used to interpolate the displacement field $u$ between the corresponding landmarks. When ${\mathcal L}= \nabla^2$, the problem reduces to the thin-plate spline image registration problem given by

$$C = \int_{\Omega} \vert\vert\nabla^2 u(x)\vert\vert^2 dx = \sum_{i=1}^{2} \int_{\Omega} \left( \frac{\partial^2 u_i(x)}{\partial^2 x_1} \right)^2$$

$$+2 \left( \frac{\partial^2 u_i(x)}{\partial x_1 \partial x_2} \right) +\left( \frac{\partial^2 u_i(x)}{\partial^2 x_2} \right)^2 dx_1 dx_2$$ (2)

subject to the constraints that $u(p_i) = q_i - p_i$ for $i = 1, \ldots, M$.

It is well known [1,2,23] that the thin-plate spline displacement field $u(x)$ that minimizes the bending energy defined by Eq. 2 has the form

$$u(x)=\sum_{i=1}^{M} \xi_i \phi(x-p_i) + A x + b.$$ (3)

where $\phi(r)=r^2 \log r$ and $\xi_i$ are $2 \times 1$ weighting vectors. The $2 \times 2$ matrix $A = [a_1, a_2]$ and the $2 \times 1$ vector $b$ define the affine transformation where $a_1$ and $a_2$ are $2 \times 1$ vectors. The procedure used to determine these unknown constants is described in Appendix A.

The thin-plate spline interpolant $\phi(r)=r^2 \log r$ is derived assuming infinite boundary conditions, i.e., $\Omega$ is assumed to be the whole plane $R^2$. The thin-plate spline transformation is truncated at the image boundary when it is applied to an image. This presents a mismatch in boundary conditions at the image edges when comparing forward and reverse transformations between two images. It also implies that a thin-plate spline transformation is not a one-to-one and onto mapping between two image spaces. To overcome this problem and to match the periodic boundary conditions assumed by the intensity-based consistent image registration algorithm [32,34], we use the following procedure to approximate periodic boundary conditions for the thin-plate spline algorithm. In the future we plan to replace the following periodic approximation method with an exact solution for the periodic landmark matching. This will be important for extending the algorithm from 2D to 3D since the computation time and storage requirements increase by a factor of 27 for the 3D case.

It is assumed for all of the algorithms presented in this paper that the images being matched have the same field of view and that they contain the same structures. We further assume that the objects in the images are centered within the image and are padded with the background intensity.

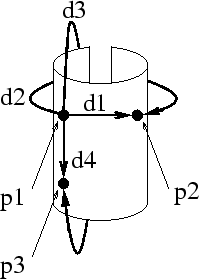
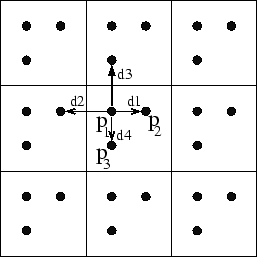
Figure 2 illustrates the concept of periodic boundary conditions for the landmark thin-plate spline registration problem. Cyclic boundary conditions implies a toroidal coordinate system such that the left-right and top-bottom boundaries of the domain $\Omega$ are mapped together. Modifying the boundary conditions in this manner causes an infinite number of interactions between landmarks for a given finite set of landmark points. Panel $(b)$ shows two such interactions between landmark points $p_1$ and $p_2$; one within the domain $\Omega$ and another between adjacent image domains. We approximate the solution of Laplace's Equation with periodic boundary conditions by solving the TPS registration problem with replicated landmark locations in the eight adjacent domains as shown in panel $(b)$ of Fig. 2. This provides a good approximation to periodic boundary conditions since the the kernel function, $\phi(r)=r^2 \log r$, causes interactions between landmarks to decrease rapidly as the distance between landmarks increases.

Figure 2: Diagrams describing the coordinate system and points used to ensure that the resulting displacement field demonstrates continuous periodic boundary conditions. The left panel is a depiction of the toroidal coordinate system. The right panel shows the layout of the point used to solve the thin-plate spline with approximate circular boundaries.

$(a)$

$(b)$

In our tests, there were differences between the transformations found using infinite and periodic boundary conditions but there was nearly no difference in terms of the magnitude of the landmark errors. The major differences between the two sets of boundary conditions was in the location of the maximum inverse consistency error. The maximum inverse consistency error was located on the image boundaries in the case of infinite boundary conditions while it was away from the boundaries for the case of periodic boundary conditions.

The inverse consistency error of the forward and reverse transformations generated by the UL-TPS can be made smaller by averaging the forward transformation with the inverse of the reverse transformation. This averaging will be referred to as the averaged unidirectional landmark-based thin-plate spline (AUL-TPS) algorithm and is used to initialize the consistent landmark TPS algorithm described in the next section. Note that this procedure does not significantly effect the error at the landmarks since the displacement at the landmark locations in the forward, reverse, inverse-forward, and inverse-reverse transformations are nearly zero as computed by the UL-TPS algorithm.

Copyright © 2002 • The University of Iowa. All rights reserved. Iowa City, Iowa 52242
Questions or Comments: gary-christensen@uiowa.edu