
 |
|||||
 |
|||||
Next: Bibliography Up: index Previous: Acknowledgments
Estimating Thin-plate Spline Parameters
The unknown UL-TPS parameters
![]() in Eq. 3
are determined by solving the linear system of equations that result by
fixing the displacement field values at landmark locations. Let
in Eq. 3
are determined by solving the linear system of equations that result by
fixing the displacement field values at landmark locations. Let
![]() and build the matrix
and build the matrix
where
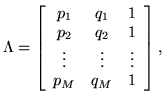 is a
is a
Next: Bibliography Up: index Previous: Acknowledgments Xiujuan Geng 2002-07-04
Copyright © 2002 • The University of Iowa. All rights reserved.
Iowa City, Iowa 52242
Questions or Comments: gary-christensen@uiowa.edu
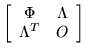
![$\displaystyle \Lambda = \left[ \begin{array}{ccc}
p_{1} & q_{1} & 1 \\
p_{2} &...
...& 1 \\
\vdots & \vdots & \vdots \\
p_{M} & q_{M} & 1 \\
\end{array}\right] ,$](img145.png)