
 |
|||||
 |
|||||
Next: Appending the Consistent Landmark Up: Methods Previous: Consistent Landmark Thin-Plate Spline
Consistent Intensity-based Registration
The consistent intensity-based registration (CI-TPS) algorithm [32,34,33] using thin-plate spline regularization
is briefly described here. It is based on minimizing the cost function
given by
The intensities of
The cost function in Eq. 6
is discretized to numerically minimize it. The forward and reverse transformations
![]() and
and ![]() and their associated displacement fields
and their associated displacement fields ![]() and
and ![]() are parameterized by the discrete Fourier series defined by
are parameterized by the discrete Fourier series defined by
for
The intensity similarity component of the cost function is forced to register the global intensity patterns before local intensity patterns by restricting the similarity gradient to modify only the low frequencies of the displacement field parameters. Restricting the similarity cost gradient to modifying the low frequency components is analogous to filtering with a zonal low-pass filter. To mitigate the Gibbs ringing associated with zonal low-pass filters, a low-pass Butterworth filter is applied to the similarity cost gradient in the gradient decent algorithm.
Next: Appending the Consistent Landmark Up: Methods Previous: Consistent Landmark Thin-Plate Spline Xiujuan Geng 2002-07-04
Copyright © 2002 • The University of Iowa. All rights reserved.
Iowa City, Iowa 52242
Questions or Comments: gary-christensen@uiowa.edu
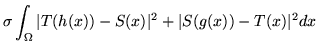
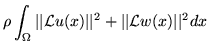
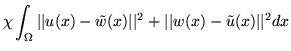
![$\displaystyle \sum_{k \in \Omega_d} \mu[k] e^{j<n,\theta [k]>}$](img106.png) and
and![$\displaystyle \sum_{k \in \Omega_d} \eta[k] e^{j<n,\theta [k]>}$](img109.png)