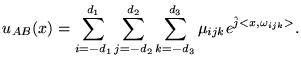|
|||||
 |
|||||
Next: Phantom, CT, and MRI Up: Image Registration Previous: Consistent Linear-elastic Registration Algorithm
Transformation Parameterization
A 3D Fourier series representation[32,16] was used to parameterize the forward
and reverse displacement fields ![]() and
and ![]() . It is assumed that the images
. It is assumed that the images ![]() and
and ![]() are represented as
are represented as
![]() voxel volumes. The displacement fields are
defined to have the form
voxel volumes. The displacement fields are
defined to have the form
where
In practice, we estimate the low frequency basis coefficients before
the higher ones allowing the global image features to be registered before
the local features. The values of ![]() ,
, ![]() , and
, and ![]() are initially set small and are periodically increased throughout
the iterative minimization procedure. The value of
are initially set small and are periodically increased throughout
the iterative minimization procedure. The value of ![]() is restricted to be less than
is restricted to be less than
![]() because that is the maximum spatial frequency basis coefficient
realizable in the FFT representation. The limits on the other two summations
are changed in a similar fashion.
because that is the maximum spatial frequency basis coefficient
realizable in the FFT representation. The limits on the other two summations
are changed in a similar fashion.
Gary E. Christensen 2002-07-04
Copyright © 2002 • The University of Iowa. All rights reserved.
Iowa City, Iowa 52242
Questions or Comments: gary-christensen@uiowa.edu