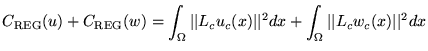|
|||||
 |
|||||
Next: Transformation Parameterization Up: Registration Algorithm Previous: Inverse Consistency Constraint
Regularization Constraint
Minimizing the cost function in (3)
does not ensure that the transformations ![]() and
and ![]() are diffeomorphic transformations except for when
are diffeomorphic transformations except for when
![]() . Continuum mechanical models such as linear elasticity
[28,22] and viscous fluid [22,15] can be used
to regularize the transformations. In this work, a linear-elastic constraint
of the form
. Continuum mechanical models such as linear elasticity
[28,22] and viscous fluid [22,15] can be used
to regularize the transformations. In this work, a linear-elastic constraint
of the form
is used to regularize the transformations where
The purpose of the regularization constraint is to ensure that the transformations
maintain the topology of the images ![]() and
and ![]() . Thus, the elasticity constraint can be replaced by or combined with
other regularization constraints that maintain desirable properties of
the template (source) and target when deformed. An example would be a
constraint that prevented the Jacobian of both the forward and reverse
transformations from going to zero or infinity. A constraint that penalizes
small and large Jacobian values is given by
. Thus, the elasticity constraint can be replaced by or combined with
other regularization constraints that maintain desirable properties of
the template (source) and target when deformed. An example would be a
constraint that prevented the Jacobian of both the forward and reverse
transformations from going to zero or infinity. A constraint that penalizes
small and large Jacobian values is given by
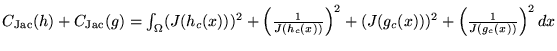 where
where ![]() denotes the Jacobian operator. Further examples of regularization
constraints that penalize large and small Jacobians can be found in Ashburner
et al. [21].
denotes the Jacobian operator. Further examples of regularization
constraints that penalize large and small Jacobians can be found in Ashburner
et al. [21].
Next: Transformation Parameterization Up: Registration Algorithm Previous: Inverse Consistency Constraint Xiujuan Geng 2002-07-04
Copyright © 2002 • The University of Iowa. All rights reserved.
Iowa City, Iowa 52242
Questions or Comments: gary-christensen@uiowa.edu