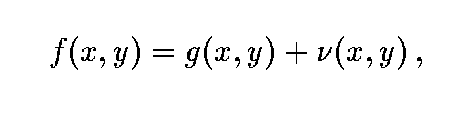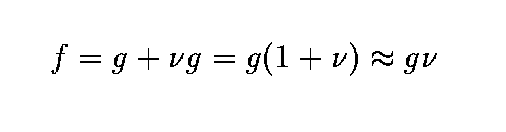55:148 Digital Image Processing
Chapter 2, Part III
Digitized image and its properties: Digital image properties
Related Reading
Sections from Chapter 2 according to the WWW Syllabus.
Chapter 2.3 Overview:
Digital image properties
Metric and topological properties of
digital images
- Some intuitively clear properties of continuous images have no straightforward analogy
in the domain of digital images
Metric properites of digital images
- Distance is an important example.
- The distance between two pixels in a digital image is a significant quantitative
measure.
- The distance between points with co-ordinates (i,j) and (h,k) may be defined in several
different ways;
- the Euclidean distance is defined by Eq. 2.42
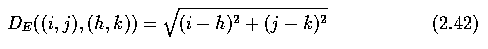
- city block distance ... Eq. 2.43
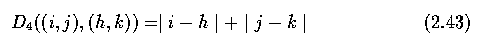
- chessboard distance Eq. 2.44
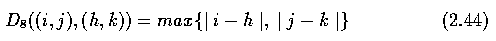
- Pixel adjacency is another important concept in digital images.
- 4-neighborhood
- 8-neighborhood (Fig. 2.6)
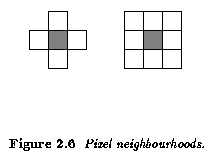
- It will become necessary to consider important sets consisting of several adjacent
pixels -- regions.
- Region is a contiguous set.
- Contiguity paradoxes of the square grid ... Figures 2.7, 2.8

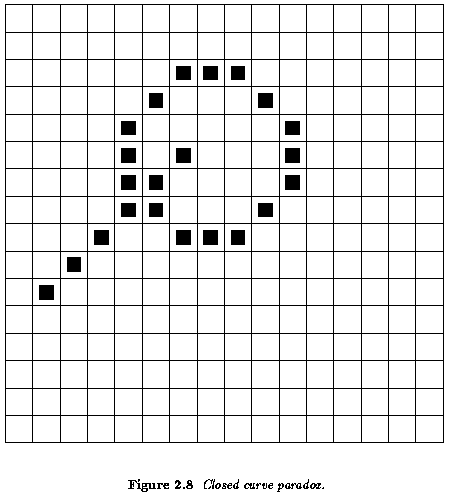
- One possible solution to contiguity paradoxes is to treat objects using 4-neighborhood
and background using 8-neighborhood (or vice versa).
- A hexagonal grid solves many problems of the square grids ... any point in the hexagonal
raster has the same distance to all its six neighbors.
- Border R is the set of pixels within the region that have one or more neighbors
outside R ... inner borders, outer borders exist.
- Edge is a local property of a pixel and its immediate neighborhood --it is a
vector given by a magnitude and direction.
- The edge direction is perpendicular to the gradient direction which points in the
direction of image function growth.
- Border and edge ... the border is a global concept related to a region, while
edge expresses local properties of an image function.
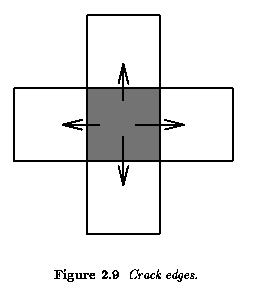
- Crack edges ... four crack edges are attached to each pixel, which are defined by
its relation to its 4-neighbors. The direction of the crack edge is that of increasing
brightness, and is a multiple of 90 degrees, while its magnitude is the absolute
difference between the brightness of the relevant pair of pixels. (Fig. 2.9)
Topological properties of digital images
- Topological properties of images are invariant to rubber sheet transformations.
- Stretching does not change contiguity of the object parts and does not change the number
of holes in regions.
- One such image property is the Euler--Poincare characteristic defined as the difference
between the number of regions and the number of holes in them.
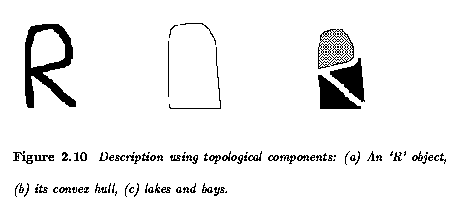
- Convex hull is used to describe topological properties of objects.
- The convex hull is the smallest region which contains the object, such that any two
points of the region can be connected by a straight line, all points of which belong to
the region.
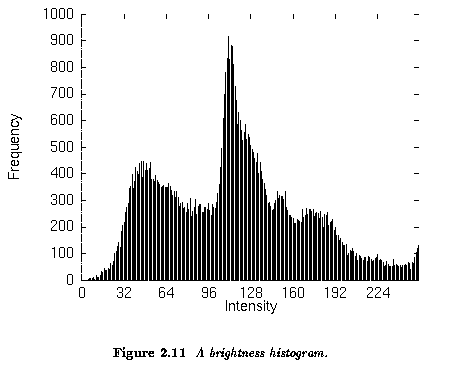
Histograms
- Brightness histogram provides the frequency of the brightness value z in the
image.
- Assign zero values to all elements of the array h.
- For all pixels (x,y) of the image f, increment h(f(x,y)) by one.
- Histograms may have many local maxima ... histogram smoothing
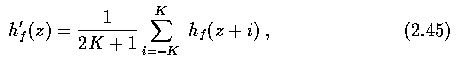
Practical Experiment 2.C - VIP Version
- Start VIP
- You have 3 minutes to complete the following exploratory exercise:
- Open the Histogram project
- Running the project displays histograms of the original image and the equalized
image.
- Analyzing the image and histogram differences, can you describe the functionality of
the histogram equalization block?
Practical Experiment 2.C - Khoros Version
- Start cantata
- You have 3 minutes to complete the following exploratory exercise:
- Open the Histogram workspace
- Display histograms of the original image and the equalized image using the histogram
display capabilities of cantata. You will find the histogram glyph under DataManip ->
HistogramOper -> Histogram. Histogram is a single-dimensional array, so you have to use
2D-Plot glyph to display the results, 2D-Plot can be found under Visualization ->
PlotDisplay -> 2D-Plot
- Analyzing the image and histogram differences, can you describe the functionality of
the histogram equalization block?
Visual perception of the image
Image quality
Noise in images
- Images are often degraded by random noise.
- Noise can occur during image capture, transmission or processing, and may be dependent
on or independent of image content.
- Noise is usually described by its probabilistic characteristics.
- White noise - constant power spectrum (its intensity does not decrease with
increasing frequency); very crude approximation of image noise
- Gaussian noise is a very good approximation of noise that occurs in many
practical cases
- probability density of the random variable is given by the Gaussian curve;
- 1D Gaussian noise - µ is the mean and
 is the standard deviation of the random variable.
is the standard deviation of the random variable.
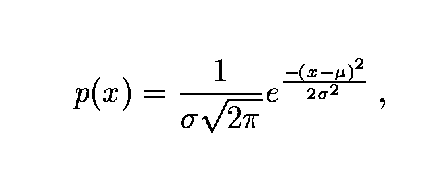
- During image transmission, noise which is usually independent of the image signal
occurs.
- Noise may be
additive, noise  and image signal g are independent
and image signal g are independent
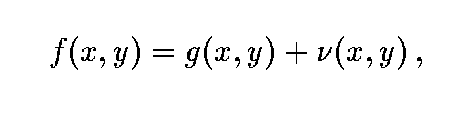
multiplicative, noise is a function of signal magnitude
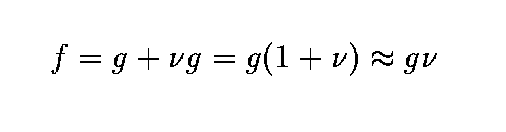
impulse noise (saturated = salt and pepper noise)
Practical Experiment 2.D - VIP Version
- Since VIP does not have the noise generation capability that Khoros does, examine the
following images that represent how noise affects images:
Practical Experiment 2.D - Khoros Version
- Start cantata
- Open the noise workspace, its filename is:
~dip/.public_html/examples/khoros.dir/noise.wksp
- Explore different parameters of the Gaussian noise, view the noise image and the
image after additive or multiplicative noise has corrupted the image. What can you
conclude? Which noise conditions corrupt the image more severely? Which noise is more
serious, additive or multiplicative?
- If you have time, choose some other noise generator from DataManip -> IntroNoise
-> (select) and continue in your explorations.
[Back one section]
[Table of Contents] [Next Chapter]
Last Modified: September 3,1996 by Milan Sonka
![[Go Back]](../IMAGES/next.gif)
![]()
![]()
![]()
![]()
![]()
![]()
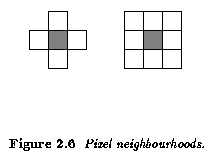





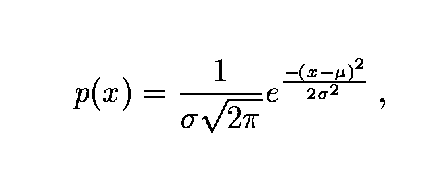
![]() and image signal g are independent
and image signal g are independent