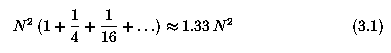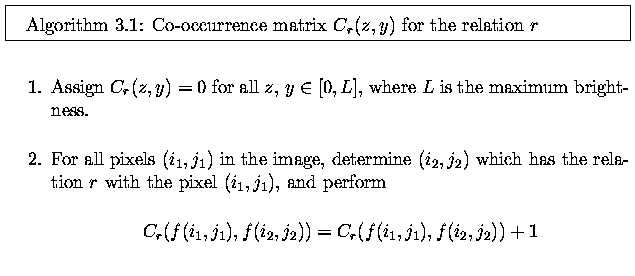55:148 Digital Image Processing
Chapter 3, Data Structures in Image Analysis
Related Reading
Sections from Chapter 3 according to the WWW Syllabus.
Chapter 3 Overview:
- Computer program = data + algorithm
- Data organization can considerably affect the simplicity of the selection and the
implementation of an algorithm. The choice of data structures is fundamental when writing
a program
Levels of image data representation
- Iconic images - consists of images containing original data; integer matrices
with data about pixel brightness.
- E.g., outputs of pre-processing operations (e.g., filtration or edge sharpening) used
for highlighting some aspects of the image important for further treatment.
- Segmented images - parts of the image are joined into groups that probably belong
to the same objects.
- It is useful to know something about the application domain while doing image
segmentation; it is then easier to deal with noise and other problems associated with
erroneous image data.
- Geometric representations - hold knowledge about 2D and 3D shapes.
- The quantification of a shape is very difficult but very important.
- Relational models - give the ability to treat data more efficiently and at a
higher level of abstraction.
- A priori knowledge about the case being solved is usually used in processing of this
kind.
- Example - counting planes standing at an airport using satellite images
- A priori knowledge
- position of the airport (e.g., from a map)
- relations to other objects in the image ( e.g., to roads, lakes, urban areas)
- geometric models of planes for which we are searching
- etc.
Traditional image data structures
- matrices,
- chains,
- graphs,
- lists of object properties,
- relational databases,
- etc.
- used not only for the direct representation of image information, also a basis of more
complex hierarchical methods of image representation.
Matrices
- Most common data structure for low level image representation Elements of the matrix are
integer numbers
- Image data of this kind are usually the direct output of the image capturing device,
e.g., a scanner.
Chains
- Chains are used for description of object borders
- Symbols in a chain usually correspond to the neighborhood of primitives in the image.
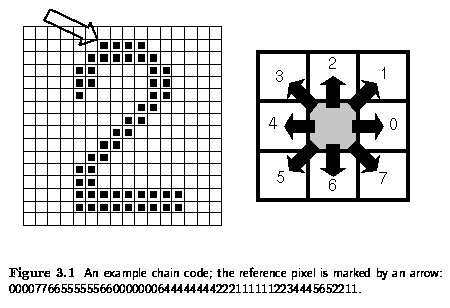
- If local information is needed from the chain code, it is necessary to search through
the whole chain systematically.
- Does the border turn somewhere to the left by 90 degrees?
- A sample pair of symbols in the chain must be found - simple.
- If global information is needed, situation is much more difficult.
- Questions about the shape of the border represented by chain codes are not trivial.
- Chains can be represented using static data structures (e.g., 1D arrays); their size is
the longest length of the chain expected.
- Dynamic data structures are more advantageous to save memory.
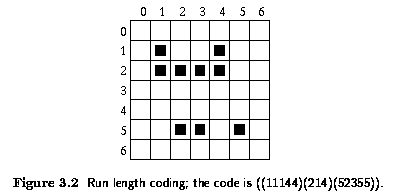
Run length coding
- often used to represent strings of symbols in an image matrix (e.g., FAX machines use
it).
- In binary images, run length coding records only areas that belong to the object in the
image; the area is then represented as a list of lists.
- Each row of the image is described by a sublist, the first element of which is the row
number.
- Subsequent terms are co-ordinate pairs; the first element of a pair is the beginning of
a run and the second is the end.
- There can be several such sequences in the row.
- Run length coding can be used for an image with multiple brightness levels as well - in
the sublist, sequence brightness must also be recorded.
Topological data structures
- Image description as a set of elements and their relations.
- Graphs
- Evaluated graphs
- Region adjacency graphs
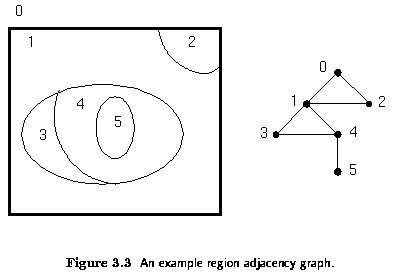
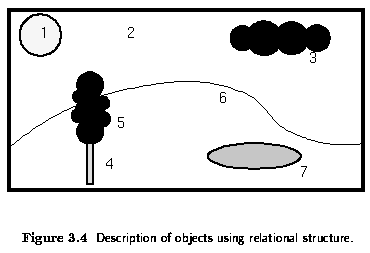
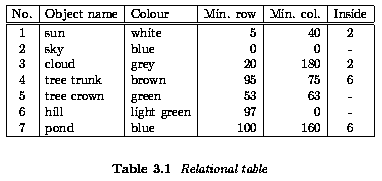
Relational structures
- information is then concentrated in relations between semantically important parts of
the image - objects - that are the result of segmentation
- Appropriate for higher level image understanding
Hierarchical data structures
- Computer vision is by its nature very computationally expensive, if for no other reason
than the amount of data to be processed.
- One of the solutions is using parallel computers = brute force
- Many computer vision problems are difficult to divide among processors, or decompose in
any way.
- Hierarchical data structures make it possible to use algorithms which decide a strategy
for processing on the basis of relatively small quantities of data.
- They work at the finest resolution only with those parts of the image for which it is
necessary, using knowledge instead of brute force to ease and speed up the processing.
- Two typical structures - pyramids and quadtrees.
Pyramids
- M-pyramid - Matrix pyramid ... is a sequence {ML, ML-1,
..., M0} of images
- ML has the same dimensions and elements as the original image
- Mi-1 is derived from the Mi by reducing the resolution by one
half.
- Square matrices with dimensions equal to powers of two required - M0
corresponds to one pixel only.
- M-pyramids are used when it is necessary to work with an image at different resolutions
simultaneously.
- An image having one degree smaller resolution in a pyramid contains four times less
data, so that it is processed approximately four times as quickly.
- Often it is advantageous to use several resolutions simultaneously rather than to choose
just one image from the M-pyramid.
- Such images can be represented using tree pyramids ... T-pyramids.
- T-pyramid is a tree, every node of the T-pyramid has 4 child nodes.
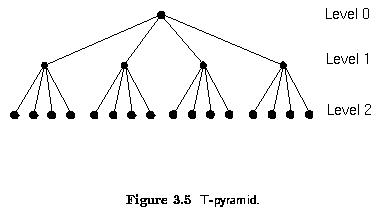
- The number of image pixels used by an M-pyramid for storing all matrices is
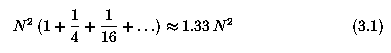
- The T-pyramid is represented in memory similarly.
- Arcs of the tree need not be recorded because addresses of the both child and parent
nodes are easy to compute due to the regularity of the structure. An algorithm for the
effective creation
3.3.1 - Quadtrees
- Quadtrees are modifications of T-pyramids.
- Every node of the tree except the leaves has four children (NW: north-western, NE:
north-eastern, SW: south-western, SE: south-eastern).
- Similarly to T-pyramids, the image is divided into four quadrants at each hierarchical
level, however it is not necessary to keep nodes at all levels.
- If a parent node has four children of the same value (e.g., brightness), it is not
necessary to record them.
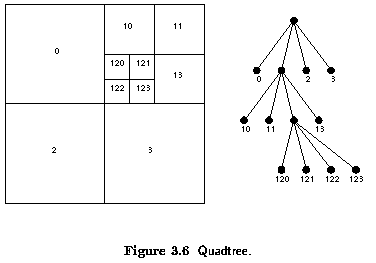
- Problems associated with hierarchical image representation:
- Dependence on the position, orientation and relative size of objects.
- Two similar images with just very small differences can have very different pyramid or
quadtree representations.
- Even two images depicting the same, slightly shifted scene, can haveentirely different
representations.
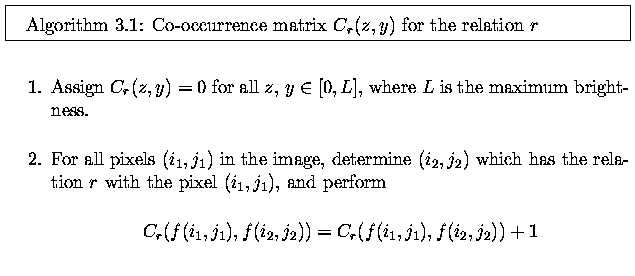
[Back one section]
[Table of Contents] [Next Chapter]
Last Modified: August 28,1997
![[Go Back]](../IMAGES/next.gif)