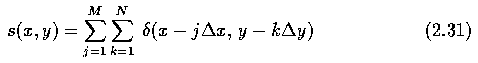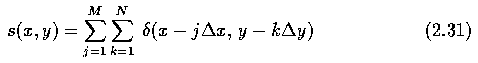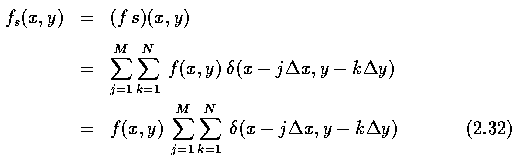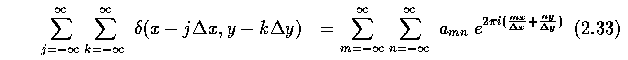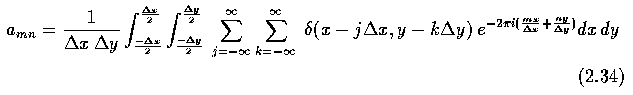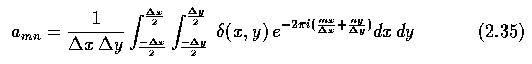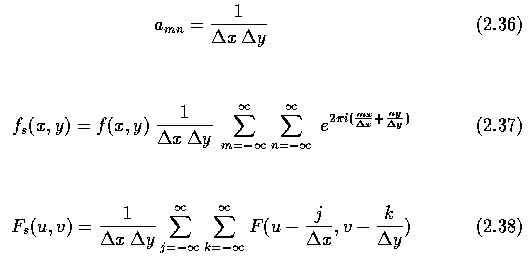55:148 Digital Image Processing

Chapter 2, Part II
Digitized image and its properties: Image digitization

Related Reading
Sections from Chapter 2 according to the WWW Syllabus.

Chapter 2.2 Overview:

Sampling PE 2.B
Quantization
Color images

Image digitization

• An image captured by a sensor is expressed as a continuous function f(x,y) of two co-ordinates in the plane.

• Image digitization means that the function f(x,y) is sampled into a matrix with M rows and N columns.

• The image quantitation assigns to each continuous sample an integer value.

• The continuous range of the image function f(x,y) is split into K intervals.

• The finer the sampling (i.e., the larger M and N) and quantitation (the larger K) the better the approximation of the continuous image function f(x,y).

• Two questions should be answered in connection with image function sampling:
• First, the sampling period should be determined -- the distance between two neighboring sampling points in the image
• Second, the geometric arrangement of sampling points (sampling grid) should be set.

Sampling

• A continuous image function f(x,y) can be sampled using a discrete grid of sampling points in the plane.

• The image is sampled at points x = j ( Delta_x), y = k (Delta_y)

• Two neighboring sampling points are separated by distance Delta_x along the x axis and Delta_y along the y axis. Distances Delta_x and Delta_y are called the sampling interval and the matrix of samples constitutes the discrete image.

• The ideal sampling s(x,y) in the regular grid can be represented using a collection of Dirac distributions (Eq. 2.31)

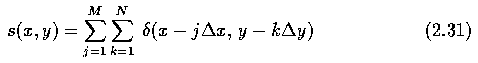
• The sampled image is the product of the continuous image f(x,y) and the sampling function s(x,y) (Eq. 2.32)

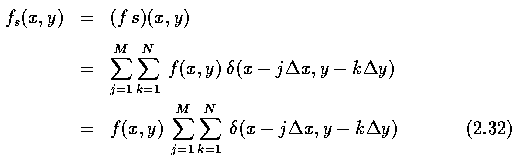
• The collection of Dirac distributions in equation 2.32 can be regarded as periodic with period x, y and expanded into a Fourier series (assuming that the sampling grid covers the whole plane (infinite limits)). (Eq. 2.33)

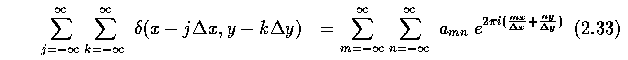
where the coefficients of the Fourier expansion can be calculated as given in Eq. 2.34

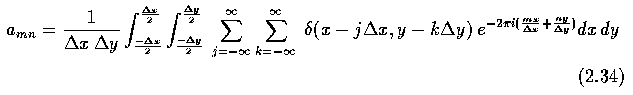
• Noting that only the term for j=0 and k=0 in the sum is nonzero in the range of integration, the coefficients are in Eq. 2.35

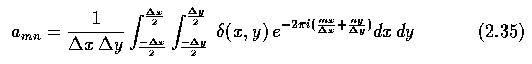
• Noting that the integral in equation 2.35 is uniformly equal to one the coefficients can be expressed as given in Eq. 2.36 and 2.32 can be rewritten as Eq. 2.37.
• In frequency domain then Eq. 2.38.

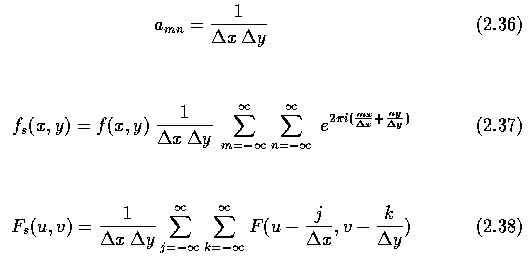
• Thus the Fourier transform of the sampled image is the sum of periodically repeated Fourier transforms F(u,v) of the image.

• Periodic repetition of the Fourier transform result F(u,v) may under certain conditions cause distortion of the image which is called aliasing; this happens when individual digitized components F(u,v) overlap.

• There is no aliasing if the image function f(x,y) has a band limited spectrum ... its Fourier transform F(u,v)=0 outside a certain interval of frequencies |u| > U; |v| > V.

• As you know from general sampling theory, overlapping of the periodically repeated results of the Fourier transform F(u,v) of an image with band limited spectrum can be prevented if the sampling interval is chosen according to Eq. 2.39

• This is the Shannon sampling theorem that has a simple physical interpretation in image analysis: The sampling interval should be chosen in size such that it is less than or equal to half of the smallest interesting detail in the image.

• The sampling function is not the Dirac distribution in real digitizers -- narrow impulses with limited amplitude are used instead.

• As a result, in real image digitizers a sampling interval about ten times smaller than that indicated by the Shannon sampling theorem is used - because the algorithms for image reconstruction use only a step function.

• Practical examples of digitization using a flatbed scanner and TV cameras help to understand the reality of sampling.

Practical Experiments

The following web sites explore the concept of aliasing in images.

• The following web site has two java applets that demonstrates aliasing in that occurs in images. This web page was written by Edward A. Lee <eal@eecs.berkeley.edu> and Pravin Varaiya <varaiya@eecs.berkeley.edu> at the University of California, Berkeley for the course EECS 20N. http://ptolemy.eecs.berkeley.edu/eecs20/week13/moire.html
• The following web site by Vincent Scheib (www.scheib.net) and is from a graduate course given at the University of North Carolina. It demonstrates Moiré patterns produced by aliasing. http://www.scheib.net/school/238/imoire/
• The following link is to the Moiré pattern description in Wikipedia. http://en.wikipedia.org/wiki/Moir%C3%A9_pattern

Practical Experiment 2.B - VIP Version

• not available at this time - instead, examine the following cases which represent the concepts of sampling and resampling:

Practical Experiment 2.B - Khoros Version

• Now, it's time for some exploration and you have 5 minutes for that.
• Using the histogram workspace, add a Resample glyph to your workspace (you will find it in Glyphs->Data Manipulation->Size & Region Operators->Resample). Connect its output to a Display glyph. Modifying the Width and Height factors, resample the image using pixel replication. Be careful if you are using the YES option in resize dimensions, the image may become quite large. Note the pixel size changes.
• You are ready for more advanced investigation. Add one more Resample glyph in series with the first one. Using YES option in resize dimensionsÓ, decrease the image resolution to 1/n in the first resampling and subsequently increase n times. Do you see the effect of decreasing image resolution on image quality?

• A continuous image is digitized at sampling points.

• These sampling points are ordered in the plane and their geometric relation is called the grid.

• Grids used in practice are mainly square or hexagonal (Figure 2.4).

• One infinitely small sampling point in the grid corresponds to one picture element (pixel) in the digital image.

• The set of pixels together covers the entire image.

• Pixels captured by a real digitization device have finite sizes.

• The pixel is a unit which is not further divisible, sometimes pixels are also called points.

Quantization

• A magnitude of the sampled image is expressed as a digital value in image processing.

• The transition between continuous values of the image function (brightness) and its digital equivalent is called quantitation.

• The number of quantitation levels should be high enough for human perception of fine shading details in the image.

• Most digital image processing devices use quantitation into k equal intervals.

• If b bits are used ... the number of brightness levels is k=2^b.

• Eight bits per pixel are commonly used, specialized measuring devices use twelve and more bits per pixel.

Color images

Not covered.