55:148 Digital Image Processing
Chapter 2, Part I
The digitized image and its properties: Basic concepts
Related Reading
Sections from Chapter 2 according to the WWW Syllabus.
Chapter 2.1 Overview:
Basic Concepts
- Fundamental concepts and mathematical tools are introduced in this chapter which will be
used throughout the course.
- A signal is a function depending on some variable with physical meaning.
- Signals can be
- one-dimensional (e.g., dependent on time),
- two-dimensional (e.g., images dependent on two co-ordinates in a plane),
- three-dimensional (e.g., describing an object in space),
- or higher-dimensional.
- A scalar function may be sufficient to describe a monochromatic image, while vector
functions are to represent, for example, color images consisting of three component
colors.
Image functions
- The image can be modeled by a continuous function of two or three variables;
- arguments are co-ordinates x, y in a plane, while if images change in time a third
variable t might be added.
- The image function values correspond to the brightness at image points.
- The function value can express other physical quantities as well (temperature, pressure
distribution, distance from the observer, etc.).
- The brightness integrates different optical quantities - using brightness as a
basic quantity allows us to avoid the description of the very complicated process of image
formation.
- The image on the human eye retina or on a TV camera sensor is intrinsically 2D. We shall
call such a 2D image bearing information about brightness points an intensity image.
- The real world which surrounds us is intrinsically 3D.
- The 2D intensity image is the result of a perspective projection of the 3D scene.
- When 3D objects are mapped into the camera plane by perspective projection a lot of
information disappears as such a transformation is not one-to-one.
- Recognizing or reconstructing objects in a 3D scene from one image is an ill-posed
problem.
- Recovering information lost by perspective projection is only one, mainly geometric,
problem of computer vision.
- The second problem is how to understand image brightness. The only information available
in an intensity image is brightness of the appropriate pixel, which is dependent on a
number of independent factors such as
- object surface reflectance properties (given by the surface material, microstructure and
marking),
- illumination properties,
- and object surface orientation with respect to a viewer and light source.
- Some scientific and technical disciplines work with 2D images directly; for example,
- an image of the flat specimen viewed by a microscope with transparent illumination,
- a character drawn on a sheet of paper,
- the image of a fingerprint, etc.
- Many basic and useful methods used in digital image analysis do not depend on whether
the object was originally 2D or 3D.
- Much of the material in this class restricts itself to the study of such methods -- the
problem of 3D understanding is addressed in Computer Vision classes offered by the
Computer Science department.
- Related disciplines are photometry which is concerned with brightness
measurement, and colorimetry which studies light reflectance or emission depending
on wavelength.
- A light source energy distribution C(x,y,t,lambda) depends in general on image
co-ordinates (x, y), time t, and wavelength lambda.
- For the human eye and most technical image sensors (e.g., TV cameras) the brightness f
depends on the light source energy distribution C and the spectral sensitivity of the
sensor, S(lambda) (dependent on the wavelength). (Eq. 2.2)
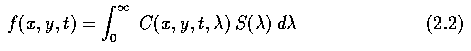
- A monochromatic image f(x,y,t) provides the brightness distribution.
- In a color or multispectral image, the image is represented by a real vector function f
(Eq. 2.3) where, for example, there may be red, green and blue components.
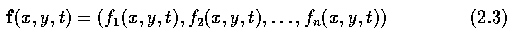
- Image processing often deals with static images, in which time t is constant.
- A monochromatic static image is represented by a continuous image function f(x,y) whose
arguments are two co-ordinates in the plane.
- Computerized image processing uses digital image functions which are usually represented
by matrices, so co-ordinates are integer numbers.
- The customary orientation of co-ordinates in an image is in the normal Cartesian fashion
(horizontal x axis, vertical y axis), although the (row, column) orientation used in
matrices is also quite often used in digital image processing.
- The range of image function values is also limited; by convention, in monochromatic
images the lowest value corresponds to black and the highest to white.
- Brightness values bounded by these limits are gray levels.
Practical Experiment 2.A - VIP Version
- At this moment, please open VIP+IDL and open the workspace histogram.vip
- You have 3 minutes to explore the gray level properties of Lena image, compare the
gray level values before and after gray level transformation.
- Are dark pixels represented by low values? What seems to be the maximum value of the
image corresponding to white? How many bits are probably used to represent the gray level
range?
Practical Experiment 2.A - Khoros Version
- At this moment, please open cantata, open your workspace histogram.wksp.
- You have 3 minutes to explore the gray level properties of Lena image, compare the
gray level values before and after gray level transformation.
- Are dark pixels represented by low values? What seems to be the maximum value of the
image corresponding to white? How many bits are probably used to represent the gray level
range?
- The quality of a digital image grows in proportion to the spatial, spectral,
radiometric, and time resolution.
- The spatial resolution is given by the proximity of image samples in the image
plane.
- The spectral resolution is given by the bandwidth of the light frequencies
captured by the sensor.
- The radiometric resolution corresponds to the number of distinguishable gray
levels.
- The time resolution is given by the interval between time samples at which images
are captured.
The Dirac distribution and convolution
The Fourier transform
Images as a stochastic process
- Images f(x,y) can be treated as deterministic functions or as realizations of stochastic
processes.
- Mathematical tools used in image description have roots in linear system theory,
integral transformations, discrete mathematics and the theory of stochastic processes.
Images as linear systems
Optical Illusions
[Back one section] [Table of Contents]
[Next Section]
Last Modified: August 28, 1997
![[Go Back]](../IMAGES/next.gif)
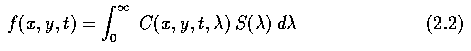
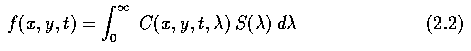
![]()