 |
APL Software |
APL Software for Operations Research
Author: Dennis Bricker
The software below was developed using APL+Win Version 3.5 (a
Rapid Application Development tool available from APL2000,
Inc.). For further information about the APL language,
see the SIGAPL web page
or Jim Weigand's web
page.
In order to use the APL workspaces below in your Windows environment,
you must first:
- install the APL run-time interpreter aplwr.exe
(Save as "application" in a directory of your choice.
If this is done corectly, the icon of the file should appear
as an inverted triangle.)
- copy the interpreter's configuration file aplwr.INI
to your Windows or WinNT directory.
- copy two files to your System folder (within
your Windows or WinNT directory): Olepro32.dll
and Msvcrt40.dll.
- If you wish to display any APL code (e.g., the dynamic programming
models in DPLIB) you should also install the APLHELP
font in your font file within your Windows directory.
Note: the four files above are compressed and must be unzipped.
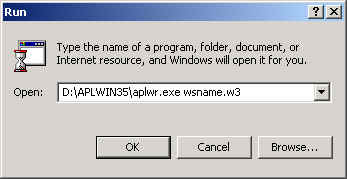
To run the code in a workspace, simply double-click or open
the workspace. A window will be opened, offering a menu from which
you can choose items. Or select "Run..." from the Start
menu, and enter the pathname of the interpreter and workspace
in the dialogue box. For example, if you have put the files in
a directory named APLWIN35 on drive D:
Please notify me if you encounter difficulties, such as the program's
terminating without warning. (It would be very helpful if you
can describe what you were doing at the time if this should happen.)
You might find the graphical user interface a bit cumbersome at
times, as I had to rewrite some of the code for the runtime version.

Copy the APL run-time workspaces into the same directory containing
the interpreter (aplwr.exe):
- ASSIGN.w3
solves "classical" linear assignment (or max-weight)
problems as well as bipartite maximum cardinality matching problems,
using algorithms appearing in the book Integer Programming,
by L. Wolsey, Chapter 4, sections 3 and 2 (pp. 55ff), respectively.
(last modified: 22 October 2001)
The user can enter data or randomly generate
problem data.
- ASTP.w3 demonstrates several
heuristic algorithms and a branch-and-bound algorithm for the
asymmetric traveling salesman problem. (last modified: 12
October 2003) The user can enter data or
randomly generate data. Algorithms include nearest neighbor,
farthest & nearest insertion, exchange algorithms, simulated
annealing, vertex penalty, as well as branch-&-bound using
assignment problem for computation of lower bounds. (Cf. also
STSP.w3 for symmetric problems.)
- BATCHDP.w3 Special-purpose
dynamic programming algorithm for computing optimal lot size
given rejection rate and setup costs. (last modified 4 March
2002)
- CPL_XD.w3
, demonstrating both Benders' decomposition and cross-decomposition
(of van Roy) algorithms applied to the capacitated plant location
problem. (last modified: 29 May 2002)
The user can enter data for the problem,
or can randomly generate problem data. See CPL_XD.pdf
and CPLXD_example.pdf
for discussion of the cross-decomposition algorithm.
- CPL.w3,
Benders' decomposition algorithm applied to the capacitated plant
location problem. Requires that student
direct each step (solving master problem & solving subproblem)
in every iteration. See CPL_XD for a more automated implementation (last modified: 3 November 2003)
The user can enter data for the problem,
or can randomly generate problem data.
- CPLGA.w3, Benders'
decomposition algorithm applied to the capacitated plant location
problem, but with the option of using a genetic algorithm to
solve the master problems.
- CTMC.w3 Analysis of continuous-time
Markov chains (last modified: 31 January 2001)
Assumes finite number of states. Computation
of steadystate distribution. User can enter problem data or randomly
generate a Markov chain.
- DEA.w3
performs Data Envelopment Analysis, providing a means of estimating
the relative efficiencies of production units.(last modified:
30 September 2001)
- DEBRUIJN.w3 computes
some (n,2) de
Bruijn sequences exhibiting some characteristics (uniformity
& balance) which may be desirable in the design of experiments.
(last modified: 15 August 2001)
- DETREP.w3 uses deterministic
dynamic programming to find the optimal replacement policy for
a machine, given cost of a new machine, trade-in
value of used machine, based upon age, and the operating cost
of a used machine, also based upon age. All parameters are assumed
to be known with certainty!(last modified: 27 November 2001).
- DPLIB.w3
General-purpose dynamic programming algorithm (both deterministic
& stochastic, with finite number of states & stages).
(last modified: 28 March 2002 ) The accompanying file DPMODELS
contains several examples, most of which allow the user to specify
parameters:
- Powerplant capacity planning
- Deterministic & stochastic production
planning with one product
- Stochastic production planning with 2
products
- Political redistricting
- One & Two-dimensional knapsack problems
- Optimal system reliability with redundant
components
- Casino problem
- Quiz show
- American option pricing
Using these pre-defined DP Models
requires that you also download DPMODELS.sf
into your directory.
- FLOWSHOP.w3 schedules
jobs in a flowshop with 2 or 3 machines (i.e., each job visits
the same sequence of machines) so as to minimize makespan. Algorithms include Johnson's algorithm and, for the
3-machine case, a branch-and-bound algorithm (last modified: 7 December 2001).
- GAP1.w3
and GAP2.w3
demonstrate two common Lagrangian relaxations (weak and strong,
respectively) of the Generalized Assignment Problem
(last modified: 18 October 2001) The user can enter data
for the problem, or can randomly generate problem data.
- GRG.w3 demonstrates the Generalized
Reduced Gradient algorithm for nonlinear minimization problems
(last modified: 12 October 2003) Unfortunately,
the run-time version does not allow the capability to enter one's
own problem definition. The files GRGTANK.sf
and GRGDAT.sf can be downloaded
to load and optimize.
- KNAP1.w3 One dimensional
knapsack problem, solved by either dynamic programming or branch-and-bound.
(last modified 17 October 2003.) The user can
enter data or randomly generate data.
- KNAP2D.w3
Two dimensional knapsack problem, solved by dynamic programming
(with 2-dimensional state space) as well as Lagrangian relaxation
and surrogate relaxation. (last modified: 22 April 2001) The user can enter data or randomly generate data.
- LCP.w3 Complementary pivoting
algorithm for solution of quadratic programming problems. (last
modified: 1 October 2003)
- LOTS.w3 Lot-sizing algorithms
for deterministic "lumpy" demand patterns: Wagner-Whitin,
Silver-Meal, Part Period Balancing, Period Order Quantity algorithms.
(last modified: 26 May 2003) The user can
enter the data or randomly generate the demand patterns.
- MARKOV.w3
Analysis of discrete-time Markov chains. (last modified: 6
February 2002 )
Assumes finite number of states. Steadystate
distribution; computation of absorption probabilities. User can
enter problem data or randomly generate a Markov chain. Includes
Markov chain model of a periodic-review (s,S) inventory system
with backordering.
- MDP.w3
Solves Markov Decision Problems with infinitely-many discrete
time periods, with either average cost/period or total discounted
cost criteria. Three algorithms are demonstrated: Value Iteration,
Policy Iteration, and Linear Programming. (last modified:
28 March 2002) The user can enter problem
data, randomly generate problem data, or provide the parameters
to generate a MDP model for an inventory replenishment application
with backordering and demand having Poisson distribution. Click
here
for presentation of sample output for the inventory replenishment
model.
- MEk1NN.w3 Analysis of
a single-server queue with finite source population and service
which is a sum of k tasks each having exponential distributions
(which may or may not be identical--if identical, service time
has an Erlang-k distribution.) (last modified: 4 March 2002)
- NETWORKS.w3
demonstrates various algorithms for (directed and undirected)
networks, e.g., shortest path, minimum spanning tree, postman
problem (last modified: 21 September 2001)
The network can be entered by the
user or randomly generated.
- PFOLIO.w3 demonstrates
complementary pivoting method for solving quadratic programming
problems deriving from portfolio selection (selecting investments
to minimize variance of return, subject to a minimum acceptable
expected rate of return, given historical data). (last modified:
3 October 2003) User can enter his/her
own data, or generate data.
- POSYGP.w3
for solution of posynomial geometric programming problems. (last modified: 5 November 2003 )
Accompanying data file containing several
pre-defined GP models is GPMODELS.sf.
- PROBLIB.w3 computes some
probability distribution functions and inverses, as well as generates
random numbers. Included are the following distributions:
Binomial, Uniform, Poisson, Exponential, Erlang, Normal, Gumbel,
Pascal, Weibull. (last modified: 24 January 2002).
- QAP.w3 demonstrates some
algorithms for the Quadratic Assignment Problem,
including simulated annealing. The user may enter his/her own
data or generate random problems. (last modified: 5 November
2003)
- QCLD1 Discrete-time one-dimensional
DP with continuous variaables, quadratic objective, and linear
transition equations. (last modified 17 March 2002)
- QCLDN
Discrete-time multi-dimensional DP with continuous variables
(QC/LD: quadratic criterion/linear dynamics). (last modified:
9 March 2002 ) (or QCLDN2,
an experimental version of QCLDN)
- QCLDAM.w3
Discrete-time control of release of water from a network of reservoirs
(application of QC/LD model). (last modified: 22 November
2003)
- RANK.w3 demonstrates a branch-and-bound
algorithm for computing a ranking of objects, given pairwise
preferences expressed by a subject, so as to minimize the number
of discrepancies (i.e., instances in which A is ranked higher
than B but B was preferred to A). (last modified: 27 September
2001)
The algorithm is described in Chapter 2 of
Graph Theory in Operations Research, by T. B. Boffey (Macmillan
Press, London) 1982.
- SEARCH.w3 contains several
algorithms for unconstrained optimization: steepest
descent, Newton's method, conjugate gradient, DFP (a quasi-Newton
method), & Powell's method. The current run-time version
does not allow you to enter the function definitions; load the
following files for some sample functions: ROSENB.sf,
NLPHW3.sf, ... (last
modified: 12 September 2003)
- SIGGP.w3 implements an
algorithm for solving signomial geometric programming problems,
using condensation to create a succession of posynomial approximations
to the signomial GP problem. The user can specify the starting
point for the algorithm, which influences the local optimum to
which the algorithm converges. No guarantee of global optimality
can be made! (last modified: 25 November 2003)
- SLPWR.w3
Two-Stage Stochastic LP with Recourse, assuming finite set of
random scenarios. (last modified: 13 May 2002) Accompanying
data files are PAR.sf,
FARM1.sf,
and FARM2.sf.
PAR is the production planning problem for golf bags,
FARM1 is the planning problem of the farmer in the problem
of Birge & Louveaux, in which the technology matrix (coefficients
of first stage variables in second stage) are random, while FARM2
is a modification of the farmer's planning problem (with random
objective and right-hand-side as well). Allows for random generation
of test problems. Click here for presentations of sample output
from the PAR
and FARM2
examples.
- SLPWSR.w3
Stochastic LP with Simple Recourse (2 stages).
(last modified: 5 May 2002)
Uses separable programming LP to find the
minimum expected cost. Assumes that only right-hand-sides are
random, with probability distributions which are either discrete,
or continuous (normal). When the probability distribution is
normal, a grid-refinement (column-generation) algorithm is used.
Allows random generation of stochastic transportation problems.
- SLPWR_SD.w3
Stochastic LP with Recourse-- Stochastic Decomposition
(last modified: 13 May 2002)
Uses Benders' decomposition to approximately
solve the problem in which the right-hand-sides are continuous
normally-distributed independent random variables. Uses the Stochastic
Decomposition algorithm of Higle and Sens. Click
here
for presentation of sample output from a stochastic transportation
problem (data file: STPC.sf)
- SOSLP.w3 Demonstrates the
restricted basis entry rule for adapting the simplex LP algorithm
to solve problems with piecewise linear functions (either convex,
concave, or neither). These functions are modeled using Special
Ordered Sets of Type 2. (Current version accepts piecewise-linear
functions in objective only.)
- STOPLOSS.w3 computes
upper & lower bounds on the stoploss insurance premium, given
past claim data in the form of numbers of claims observed in
each of a finite number of intervals (cells). The extremal distribution
yielding the upper or lower bounds may be restricted to be within
a certain "distance" of the historical claim distribution,
where "distance" may be
measured by:
> the Chi-square statistic
> the "modified" Chi-square statistic
> the I-divergence.
(Last modified: 6 June 2002.)
- STSP.w3 demonstrates several
heuristic algorithms and a branch-and-bound algorithm for the
symmetric traveling salesman problem. (last modified: 12 October
2003) The user can enter data or randomly
generate data. Algorithms include nearest neighbor, farthest
& nearest insertion, exchange algorithms, simulated annealing,
vertex penalty, as well as branch-&-bound using vertex penalty
algorithm for computation of lower bounds. (Cf. also ATSP.w3
for asymmetric problems.)
- TRIM.w3 solves the one-dimensional
"trim" or "cutting stock" problem, using
an LP model with columns generated by solving knapsack problems.
(last modified: 26 May 2003) The user
can enter data or randomly generate data.
- TRANSPORT.w3
solves the "classical" transportation problem with
or without capacity constraints on the individual shipments.
Also illustrates Vogel's Approximation Method (VAM) and Northwest-Corner
Method. (last modified: 3 October 2001) The
user can enter data or randomly generate data.
- UBT.w3 is an implementation
of the "Upper Bounding Technique", a variation of the
revised simplex method which more efficiently handles upper &/or
lower bounds on the variables.(last modified: 28 August 2002)
The current version assumes equality constraints,
so that the user must explicitly define slack &/or surplus
variables. (These can be given upper bounds in order to constrain
a linear function to lie in some bounded interval.)
- WEBER.w3 addresses Weber's
problem of locating a single facility in the plane so as to minimize
the sum of shipping costs to customers (assumed to be proportional
to Euclidean distances). A heuristic is also included for the
multi-facility location/allocation problem. (Last modified
5 November 2003.) The user can enter data or
randomly generate data.

To run the code in a workspace, simply double-click or open
the workspace. A window will be opened, offering a menu from which
you can choose items.
Please notify me if you encounter difficulties, such as the program's
terminating without warning. (It would be helpful if you can describe
what you were doing at the time if this should happen.) You might
find the graphical user interface a bit cumbersome at times, as
I had to rewrite some of the code for the runtime version.
These workspaces were written for educational purposes only,
to demonstrate the various algorithms using small examples.
 to Dennis Bricker's
home page
to Dennis Bricker's
home page
http://www.engineering.uiowa.edu/~dbricker/APL_software.html
dennis-bricker@uiowa.edu
Last modified: 31 August 2004


