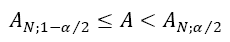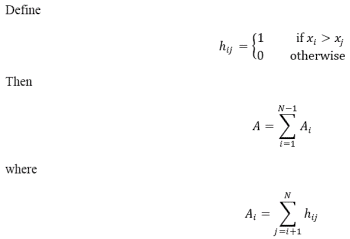
For a random variable xi, i = 1, 2, 3, ..., N, count the number of times that xi > xj for i < j. Each such inequality is called a reverse arrangement. The total number of reverse arrangement is denoted by A.
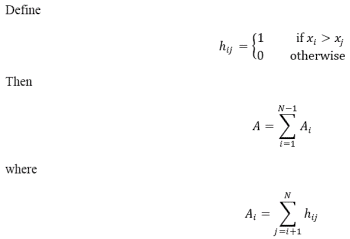
For example, consider the following sequence of N = 8 observations;
x1 = 5, x2 = 3, x3 = 8, x4 = 9, x5 = 4, x6 = 1, x7 = 7, x8 = 5
x1 > x2, x1 > x5, and x1 > x6 which gives A1 = 3
x2 > x6 which gives A2 = 1
Continuing on, A3 = 4, A4 = 4, A5 = 1, A6 = 0, A7 = 1
The total number of reverse arrangement is, therefore,
A = A1 + A2 + ... + A7 = 3 + 1 + 4 + 4 + 1 + 0 + 1 = 14
The observations are independent observations of a random variable x(k) where there in no trend.