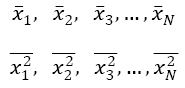
Proof of self-stationarity for individual sample records can be accepted as proof of stationarity for the random process.
Verification of weak stationarity will be acceptable, thus the verification of stationarity can be restricted to investigations of only the mean values and autocorrelation functions (i.e., variance values) for the data.
The sample record of the data to be investigated is very long compared to the random fluctuations of the data time history.
1) Divide the sample record into N equal time intervals where the data in each interval may be considered independent.
2) Compute a mean value and mean square value for each interval and align these sample values in time sequence, as follows,
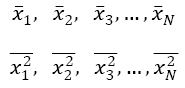
3) Test the sequence of mean and mean square values for the presence of underlying trends or variations other than those due to expected sampling variations.
Non-parametric tests which do not require a knowledge of sampling distributions for the data.
1) Run test
2) Trend test