|
|||||
 |
|||||
Next: Invertibility property Up: index Previous: Introduction
Transformation Properties
The following definitions will be used throughout the paper. Let ![]() for
for
![]() denote a set of homogeneous, topologically-equivalent
anatomical images defined on the coordinate system or domain
denote a set of homogeneous, topologically-equivalent
anatomical images defined on the coordinate system or domain
![]() . For example,
. For example, ![]() ,
, ![]() , etc., may correspond to a set of 3D MRI brain images collected
from age and sex matched normals or abnormals or some other suitable classification
criteria. Let
, etc., may correspond to a set of 3D MRI brain images collected
from age and sex matched normals or abnormals or some other suitable classification
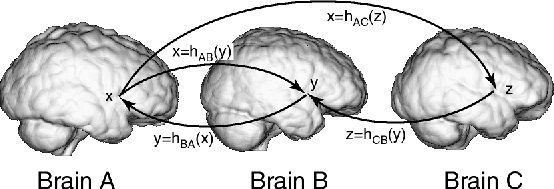
criteria. Let ![]() represent the transformation from the coordinate system of image
represent the transformation from the coordinate system of image
![]() to that of image
to that of image ![]() in terms of the coordinate system of image
in terms of the coordinate system of image ![]() as shown in Figure 1.
Let the linear transformation
as shown in Figure 1.
Let the linear transformation
![]() deform image
deform image ![]() into a new image
into a new image
![]() that resembles the shape of image
that resembles the shape of image ![]() by transforming the coordinate system of image
by transforming the coordinate system of image ![]() to that of image
to that of image ![]() . Define
. Define ![]() as the set of all transformations
as the set of all transformations ![]() for
for ![]() and
and
![]() . Let
. Let
![]() denote the standard
2-norm.
denote the standard
2-norm.
Subsections
Next: Invertibility property Up: index Previous: Introduction Gary E. Christensen 2002-07-04
Copyright © 2002 • The University of Iowa. All rights reserved.
Iowa City, Iowa 52242
Questions or Comments: gary-christensen@uiowa.edu