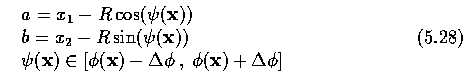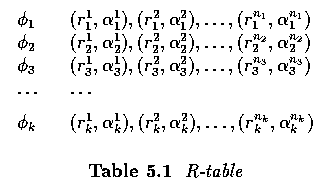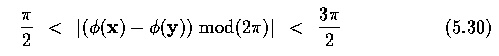55:148 Digital Image Processing
Chapter 5, Part II
Segmentation: Edge-based segmentation
Related Reading
Sections from Chapter 5 according to the WWW Syllabus.
Chapter 5.2 Overview:
Edge-based Segmentation
- Edge-based segmentation represents a large group of methods based on information about
edges in the image
- Edge-based segmentations rely on edges found in an image by edge detecting operators --
these edges mark image locations of discontinuities in gray level, color, texture, etc.
- Image resulting from edge detection cannot be used as a segmentation result.
- Supplementary processing steps must follow to combine edges into edge chains that
correspond better with borders in the image.
- The final aim is to reach at least a partial segmentation -- that is, to group local
edges into an image where only edge chains with a correspondence to existing objects or
image parts are present.
- The more prior information that is available to the segmentation process, the better the
segmentation results that can be obtained.
- The most common problems of edge-based segmentation are
- an edge presence in locations where there is no border, and
- no edge presence where a real border exists.
Edge image thresholding
- Almost no zero-value pixels are present in an edge image, but small edge values
correspond to non-significant gray level changes resulting from quantization noise, small
lighting irregularities, etc.
- Selection of an appropriate global threshold is often difficult and sometimes
impossible; p-tile thresholding can be applied to define a threshold
- Alternatively, non-maximal suppression and hysteresis thresholding can be used as was
introduced in the Canny edge detector.

Edge relaxation
- Borders resulting from the previous method are strongly affected by image noise, often
with important parts missing.
- Considering edge properties in the context of their mutual neighbors can increase the
quality of the resulting image.
- All the image properties, including those of further edge existence, are iteratively
evaluated with more precision until the edge context is totally clear - based on the
strength of edges in a specified local neighborhood, the confidence of each edge is either
increased or decreased.
- A weak edge positioned between two strong edges provides an example of context; it is
highly probable that this inter-positioned weak edge should be a part of a resulting
boundary.
- If, on the other hand, an edge (even a strong one) is positioned by itself with no
supporting context, it is probably not a part of any border.
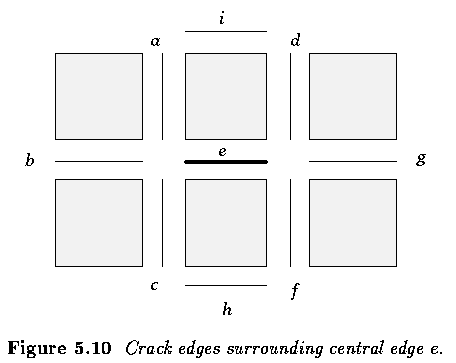
- Edge context is considered at both ends of an edge, giving the minimal edge
neighborhood.
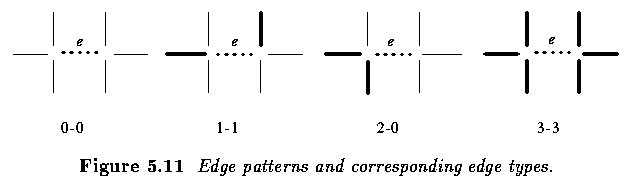
- The central edge e has a vertex at each of its ends and three possible border
continuations can be found from both of these vertices.
- Vertex type -- number of edges emanating from the vertex, not counting the edge e.
- The type of edge e can then be represented using a number pair i-j describing edge
patterns at each vertex, where i and j are the vertex types of the edge e.

- Edge relaxation is an iterative method, with edge confidences converging either to zero
(edge termination) or one (the edge forms a border).
- The confidence of each edge e in the first iteration can be defined as a normalized
magnitude of the crack edge,
- with normalization based on either the global maximum of crack edges in the whole image,
or on a local maximum in some large neighborhood of the edge


- The main steps of the above Algorithm are evaluation of vertex types followed by
evaluation of edge types, and the manner in which the edge confidences are modified.
- A vertex is considered to be of type i if
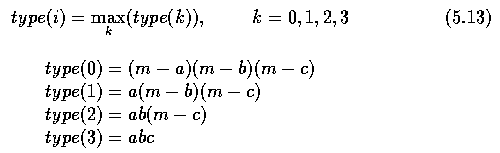
- where a,b,c are the normalized values of the other incident crack edges
- m=max(a,b,c,q) ... the introduction of the quantity q ensures that type(0) is non-zero
for small values of a.
- For example, choosing q=0.1, a vertex (a,b,c)=(0.5, 0.05, 0.05) is a type 1 vertex,
while a vertex (0.3, 0.2, 0.2) is a type 3 vertex.
- Similar results can be obtained by simply counting the number of edges emanating from
the vertex above a threshold value.
- Edge type is found as a simple concatenation of vertex types, and edge confidences are
modified as follows:
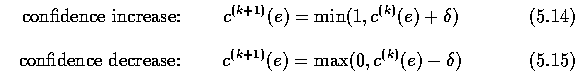
- Edge relaxation, as described above, rapidly improves the initial edge labeling in the
first few iterations.
- Unfortunately, it often slowly drifts giving worse results than expected after larger
numbers of iterations.
- The reason for this strange behavior is in searching for the global maximum of the edge
consistency criterion over all the image, which may not give locally optimal results.
- A solution is found in setting edge confidences to zero under a certain threshold, and
to one over another threshold which increases the influence of original image data.
- Therefore, one additional step must be added to the edge confidence computation
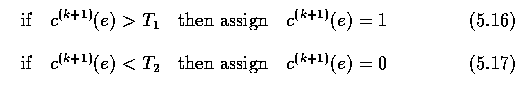
- where T_1 and T_2 are parameters controlling the edge relaxation convergence speed and
resulting border accuracy.
- This method makes multiple labeling possible; the existence of two edges at different
directions in one pixel may occur in corners, crosses, etc.
- The relaxation method can easily be implemented in parallel.
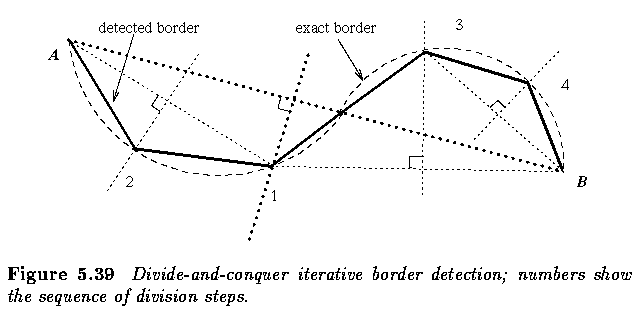
Border tracing
- If a region border is not known but regions have been defined in the image, borders can
be uniquely detected.
- First, let us assume that the image with regions is either binary or that regions have
been labeled.
- An inner region border is a subset of the region
- An outer border is not a subset of the region.
- The following algorithm covers inner boundary tracing in both 4-connectivity and
8-connectivity.


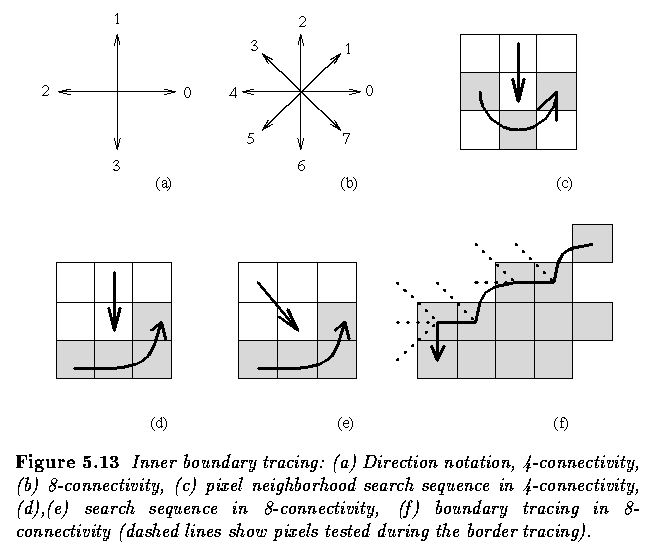
- The above Algorithm works for all regions larger than one pixel.
- Looking for the border of a single-pixel region is a trivial problem.
- This algorithm is able to find region borders but does not find borders of region holes.
- To search for hole borders as well, the border must be traced starting in each region or
hole border element if this element has never been a member of any border previously
traced.
- Note that if objects are of unit width, more conditions must be added.
- If the goal is to detect an outer region border, the given algorithm may still be
used based on 4-connectivity.
- Note that some border elements may be repeated in the outer border up to three times.
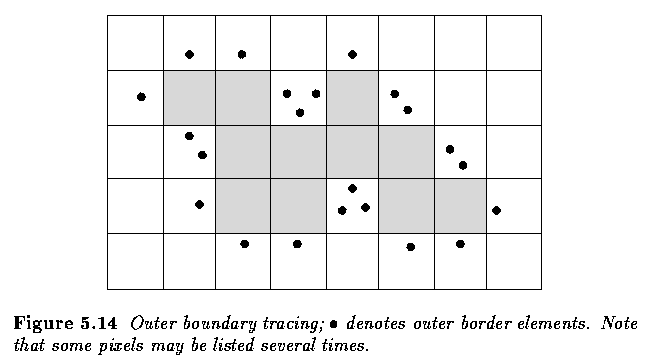

- The inner border is always part of a region but the outer border never is.
- Therefore, if two regions are adjacent, they never have a common border, which causes
difficulties in higher processing levels with region description, region merging, etc.
- The inter-pixel boundary extracted, for instance, from crack edges is common to adjacent
borders, nevertheless, its position cannot be specified in pixel co-ordinates.
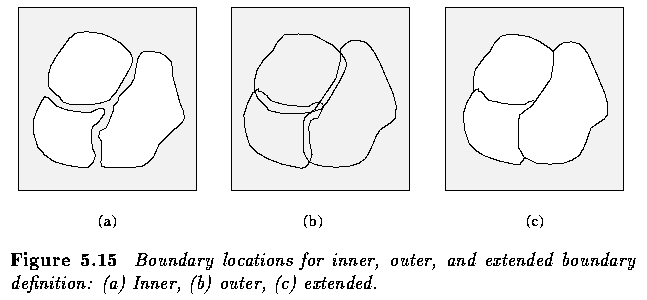
- Boundary properties better than those of outer borders may be found in extended
borders.
- single common border between adjacent regions
- may be specified using standard pixel co-ordinates
- the boundary shape is exactly equal to the inter-pixel shape but is shifted one
half-pixel down and one half-pixel right
- The extended boundary is defined using 8-neighborhoods
- e.g.P_4(P) denotes the pixel immediately to the left of pixel P
- Four kinds of inner boundary pixels of a region R are defined; if Q denotes pixels
outside the region R, then
LEFT pixel if P_4(P) in Q
RIGHT pixel if P_0(P) in Q
UPPER pixel if P_2(P) in Q
LOWER pixel if P_6(P) in Q
- Let LEFT(R), RIGHT(R), UPPER(R), LOWER(R) represent the corresponding subsets of R.
- The extended boundary EB is defined as a set of points P,P_0,P_6,P_7 satisfying the
following conditions:
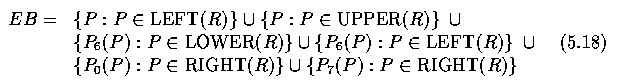
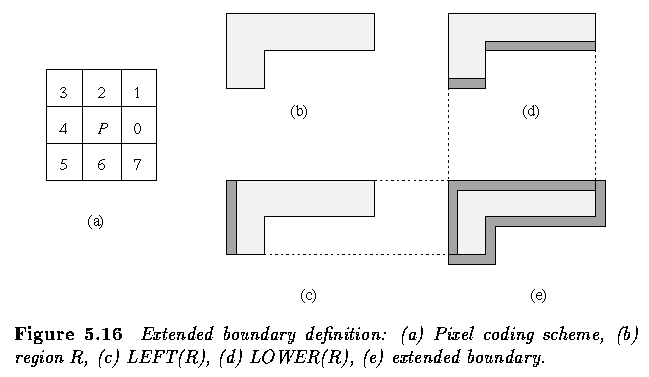
- The extended boundary can easily be constructed from the outer boundary.
- Using an intuitive definition of RIGHT, LEFT, UPPER, and LOWER outer boundary points,
the extended boundary may be obtained by shifting all the UPPER outer boundary points one
pixel down and right, shifting all the LEFT outer boundary points one pixel to the right,
and shifting all the RIGHT outer boundary points one pixel down. The LOWER outer boundary
point positions remain unchanged.
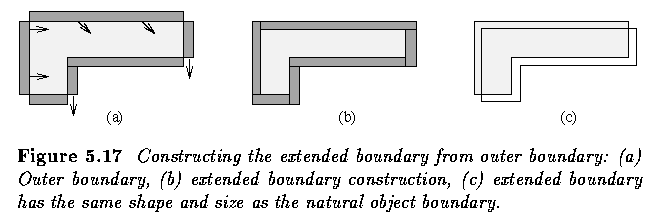
- A more sophisticated approach is based on detecting common boundary segments between
adjacent regions and vertex points in boundary segment connections.
- The detection process is based on a look-up table, which defines all 12 possible
situations of the local configuration of 2 x 2 pixel windows, depending on the previous
detected direction of boundary, and on the status of window pixels which can be inside or
outside a region.
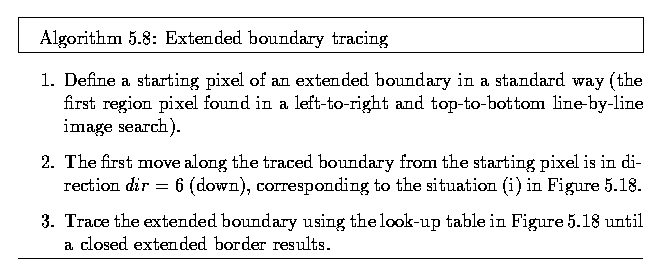
- Note that there is no hole-border tracing included in the algorithm.
- The holes are considered separate regions and therefore the borders between the region
and its hole are traced as a border of the hole.
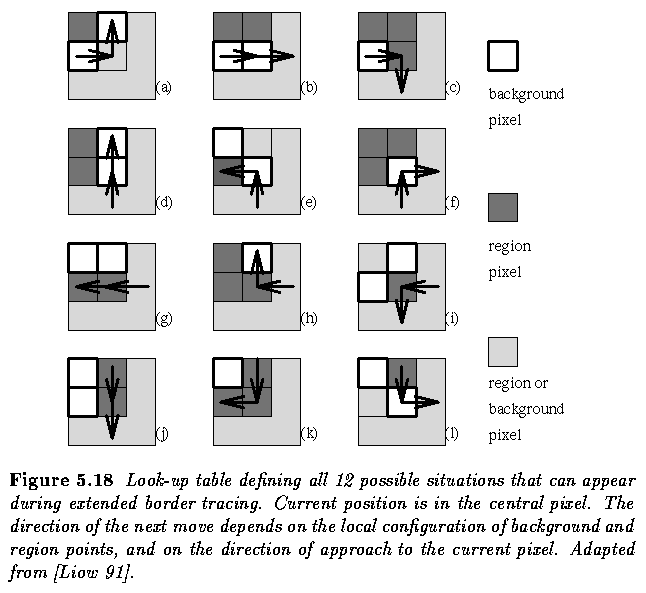
- The look-up table approach makes the tracing more efficient than conventional methods
and makes parallel implementation possible.
- In addition to extended boundary tracing, it provides a description of each boundary
segment in chain code form together with information about vertices.
- This method is very suitable for representing borders in higher level segmentation
approaches including methods that integrate edge-based and region-based segmentation
results.
- Moreover, in the conventional approaches, each border between two regions must be traced
twice. The algorithm can trace each boundary segment only once storing the information
about what has already been done in double-linked lists.
- A more difficult situation is encountered if the borders are traced in grey level images
where regions have not yet been defined.
- The border is represented by a simple path of high-gradient pixels in the image.
- Border tracing should be started in a pixel with a high probability of being a border
element, and then border construction is based on the idea of adding the next elements
which are in the most probable direction.
- To find the following border elements, edge gradient magnitudes and directions are
usually computed in pixels of probable border continuation.
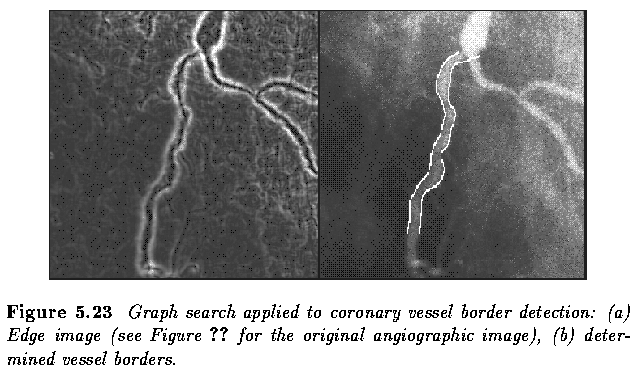
Border detection as graph searching
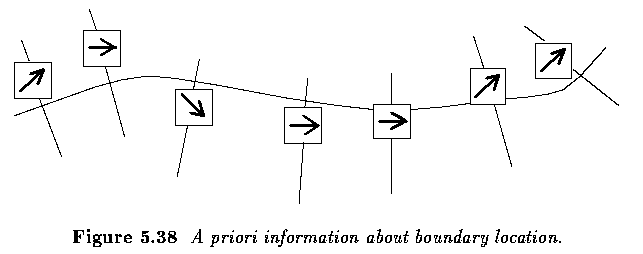
- Whenever additional knowledge is available for boundary detection, it should be used -
e.g., known approximate starting point and ending point of the border
- Even some relatively weak additional requirements such as smoothness, low curvature,
etc. may be included as prior knowledge.
- A graph is a general structure consisting of a set of nodes n_i and arcs between the
nodes [n_i,n_j]. We consider oriented and numerically weighted arcs, these weights being
called costs.
- The border detection process is transformed into a search for the optimal path in the
weighted graph.
- Assume that both edge magnitude and edge direction information is available in an edge
image.
- Figure 6.19a shows an image of edge directions, with only significant edges according to
their magnitudes listed.
- Figure 6.19b shows an oriented graph constructed in accordance with the presented
principles.
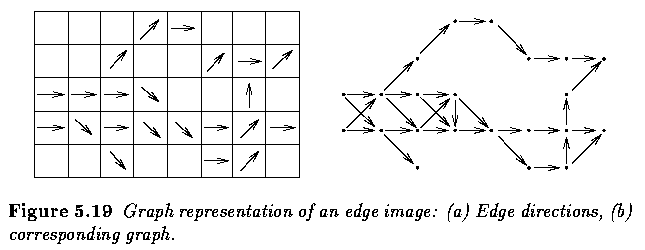
- To use graph search for region border detection, a method of oriented weighted-graph
expansion must first be defined.
Graph Search Example
- A cost function f(x_i) must also be defined that is a cost estimate of the path between
nodes n_A and n_B (pixels x_A and x_B) which goes through an intermediate node n_i (pixel
x_i).
- The cost function f(x_i) typically consists of two components; an estimate of the path
cost between the starting border element x_A and x_i, and an estimate of the path cost
between x_i and the end border element x_B.
- The cost of the path from the starting point to the node n_i is usually a sum of costs
associated with the arcs or nodes that are in the path.
- The cost function must be separable and monotonic with respect to the path length, and
therefore the local costs associated with arcs are required to be non-negative.
- If no additional requirements are set on the graph construction and search, this process
can easily result in an infinite loop.
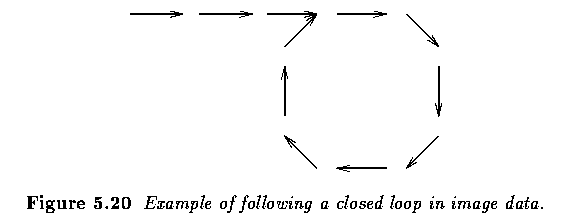
- To prevent this behavior, no node expansion is allowed that puts a node on the OPEN list
if this node has already been visited, and put on the OPEN list in the past.
- A simple solution to the loop problem is not to allow searching in a backward direction.
- It may be possible to straighten the processed image (and the corresponding graph).
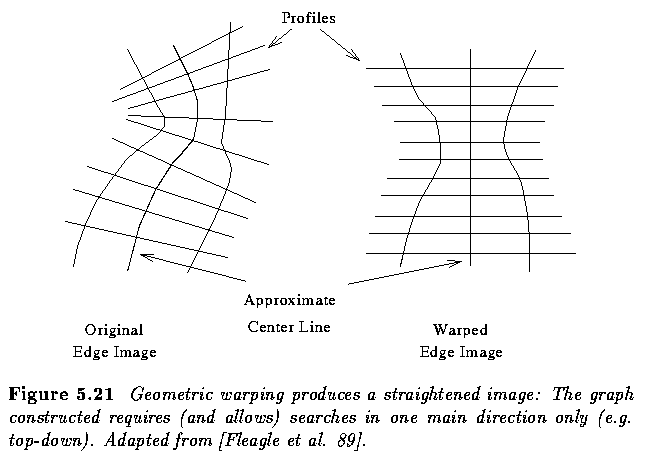
- The estimate of the cost of the path from the current node n_i to the end node n_B has a
substantial influence on the search behavior.
- If this estimate ~h(n_i) of the true cost h(n_i) is not considered, so ~h(n_i)=0, no
heuristic is included in the algorithm and a breadth-first search is done.
- The detected path will always be optimal according to the criterion used, the minimum
cost path will always be found.
- Applying heuristics, the detected cost does not always have to be optimal but the search
can often be much faster.
- The minimum cost path result can be guaranteed if ~h(n_i)<= h(n_i) and if the true
cost of any part of the path c(n_p,n_q) is larger than the estimated cost of this part
~c(n_p,n_q).
- The closer the estimate ~h(n_i) is to h(n_i), the lower the number of nodes expanded in
the search.
- The problem is that the exact cost of the path from the node n_i to the end node n_B is
not known beforehand.
- In some applications, it may be more important to get a quick rather than an optimal
solution. Choosing ~h(n_i)>h(n_i), optimality is not guaranteed but the number of
expanded nodes will typically be smaller because the search can be stopped before the
optimum is found.
- If ~h(n_i)=0, the algorithm produces a minimum-cost search.
- If ~h(n_i)<= h(n_i), the search will produce the minimum-cost path if
and only if the conditions presented earlier are satisfied.
- If ~h(n_i)= h(n_i), the search will always produce the minimum-cost path
with a minimum number of expanded nodes.
- If ~h(n_i)>h(n_i), the algorithm may run faster, but the minimum-cost
result is not guaranteed.
- The better the estimate of h(n), the smaller the number of nodes that must
be expanded.
- A crucial question is how to choose the evaluation cost functions for graph-search
border detection.
- Some generally applicable cost functions are
- Strength of edges forming a border
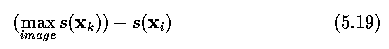
- where the maximum edge strength is obtained from all pixels in the image.

- where DIF is some suitable function evaluating the difference in edge directions in two
consecutive border elements.
- Proximity to an approximate border location

- Estimates of the distance to the goal (end-point)
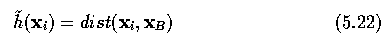
- Since the range of border detection applications is quite wide, the cost functions
described may need some modification to be relevant to a particular task.
- Graph searching techniques offer a convenient way to ensure global optimality of the
detected contour.
- The detection of closed structure contours would involve geometrically transforming the
image using a polar to rectangular co-ordinate transformation in order to `straighten' the
contour.
- Searching for all the borders in the image without knowledge of the start and end-points
is more complex.
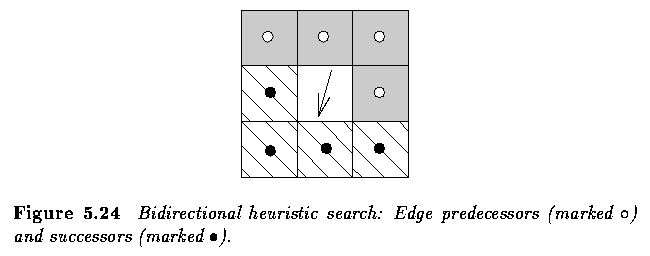
- Edge chains may be constructed by applying a bidirectional heuristic search in which
half of each 8-neighborhood expanded node is considered as lying in front of the edge, the
second half as lying behind the edge.
Border detection as dynamic programming
- Dynamic programming is an optimization method based on the principle of optimality.
- It searches for optima of functions in which not all variables are simultaneously
interrelated.
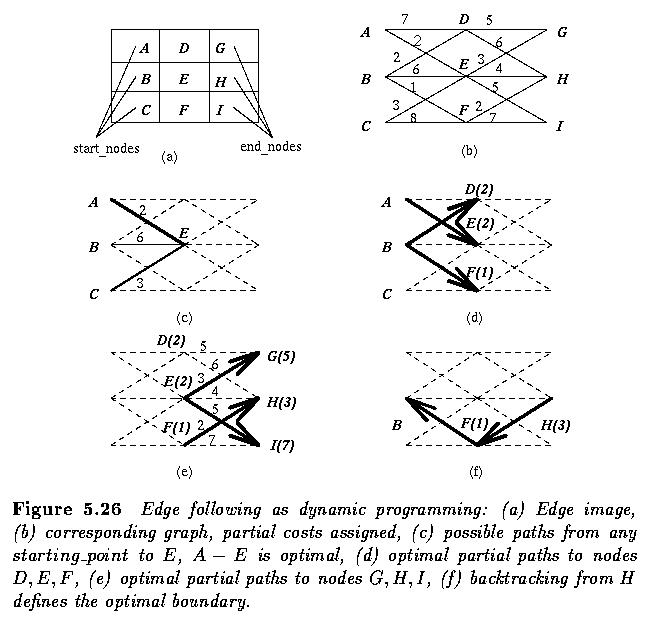
- The main idea of the principle of optimality is:
- Whatever the path to the node E was, there exists an optimal path between E and the
end-point.
- In other words, if the optimal path start-point -- end-point goes through E then both
its parts start-point -- E and E -- end-point are also optimal.
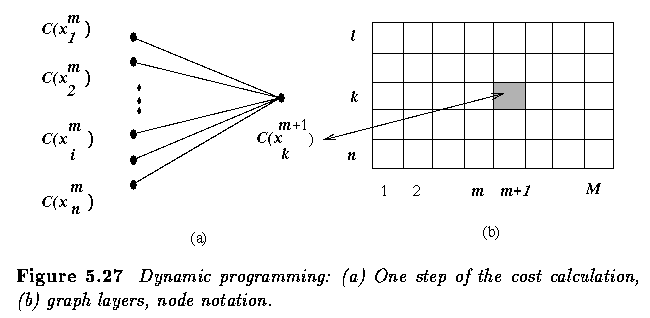
- If the graph has more layers, the process is repeated until one of the end-points is
reached.
- The complete graph must be constructed to apply dynamic programming, and this may follow
general rules given in the previous section.
- The objective function must be separable and monotonic (as for the A-algorithm);
evaluation functions presented in the previous section may also be appropriate for dynamic
programming.


- Comparisons ...
- Heuristic Graph Search vs. Dynamic Programming
- It has been shown that heuristic search may be more efficient than dynamic programming
for finding a path between two nodes in a graph if a good heuristic is available.
- A-algorithm based graph search does not require explicit definition of the graph.
- Dynamic programming presents an efficient way of simultaneously searching for optimal
paths from multiple starting and ending points.
- If these points are not known, dynamic programming is probably a better choice,
especially if computation of the partial costs g^m(i,k) is simple.
- Nevertheless, which approach is more efficient for a particular problem depends on
evaluation functions and on the quality of heuristics for an A-algorithm. A

- Live Wire, Live Lane (videotape demonstration)
- Practical border detection using two-dimensional dynamic programming was developed by
Barrett et al. and Udupa et al.
- Live wire combines automated border detection with manual definition of the
boundary start-point and interactive positioning of the end-point.
- In dynamic programming, the graph that is searched is always completely constructed at
the beginning of the search process. Therefore, interactive positioning of the end-point
invokes no time-consuming recreation of the graph as would be the case in heuristic graph
searching.
- Thus, after construction of the complete graph and associated node costs, optimal
borders connecting the fixed start-point and the interactively changing end-point can be
determined in real time.
- In the case of large or more complicated regions, the complete region border is usually
constructed from several border segments.
- In the live lane approach, an operator defines a region of interest by
approximately tracing the border by moving a square window.
- The size of the window is either preselected or is adaptively defined from the speed and
acceleration of the manual tracing. When the border is of high quality, the manual tracing
is fast and the live lane method is essentially identical to the live wire method applied
to a sequence of rectangular windows. If the border is less obvious, manual tracing is
usually slower and the window size adaptively decreases.
- If the window size reduces to a single pixel, the method degenerates to manual tracing.
- A flexible method results that combines the speed of automated border detection with the
robustness of manual border detection whenever needed.
- Since the graph is only constructed using the image portion comparable in size to the
size of the moving window, the computational demands of the live lane method are much
lower than that of the live wire method.
- Several additional features of the two live methods are worth mentioning.
- Design of border detection cost functions often requires substantial experience and
experimentation.
- To facilitate the method's usage by non-experts, an automated approach has been
developed that determines optimal border features from examples of the correct borders.
- The resultant optimal cost function is specifically designed for a particular
application and can be conveniently obtained by simply presenting a small number of
example border segments during the method's training stage.
Hough transforms
- If an image consists of objects with known shape and size, segmentation can be viewed as
a problem of finding this object within an image.
- Consider an example of circle detection.
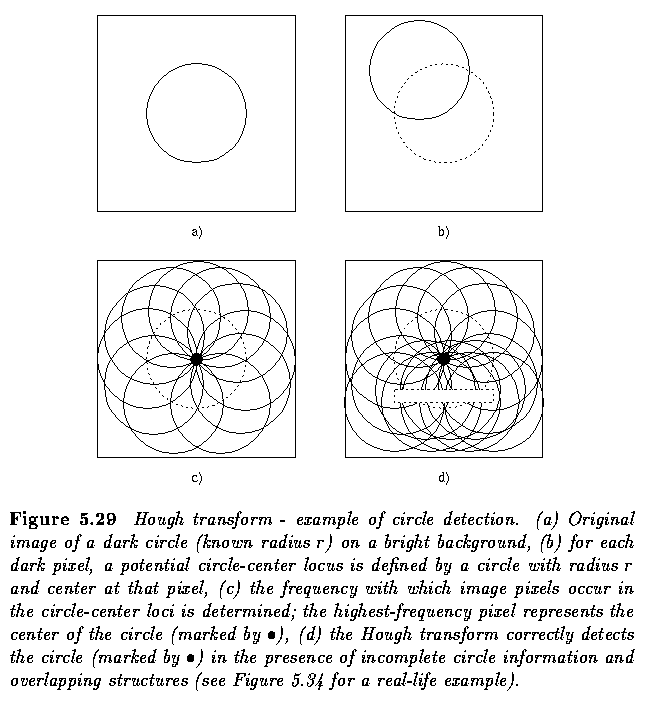
The following applet demonstrates the circular
Hough Transform and was created by Mark A. Schulze http://www.markschulze.net/.
- The original Hough transform was designed to detect straight lines and curves
- A big advantage of this approach is robustness of segmentation results; that is,
segmentation is not too sensitive to imperfect data or noise.
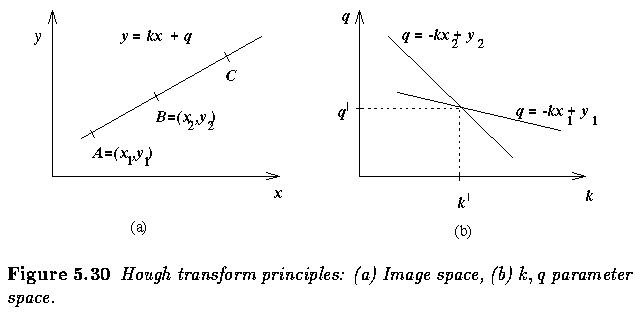
- This means that any straight line in the image is represented by a single point in the
k,q parameter space and any part of this straight line is transformed into the same point.
- The main idea of line detection is to determine all the possible line pixels in the
image, to transform all lines that can go through these pixels into corresponding points
in the parameter space, and to detect the points (a,b) in the parameter space that
frequently resulted from the Hough transform of lines y=ax+b in the image.
- Detection of all possible line pixels in the image may be achieved by applying an edge
detector to the image
- Then, all pixels with edge magnitude exceeding some threshold can be considered possible
line pixels.
- In the most general case, nothing is known about lines in the image, and therefore lines
of any direction may go through any of the edge pixels. In reality, the number of these
lines is infinite, however, for practical purposes, only a limited number of line
directions may be considered.
- The possible directions of lines define a discretization of the parameter k.
- Similarly, the parameter q is sampled into a limited number of values.
- The parameter space is not continuous any more, but rather is represented by a
rectangular structure of cells. This array of cells is called the accumulator array
A, whose elements are accumulator cells A(k,q).
- For each edge pixel, parameters k,q are determined which represent lines of allowed
directions going through this pixel. For each such line, the values of line parameters k,q
are used to increase the value of the accumulator cell A(k,q).
- Clearly, if a line represented by an equation y=ax+b is present in the image, the value
of the accumulator cell A(a,b) will be increased many times -- as many times as the line
y=ax+b is detected as a line possibly going through any of the edge pixels.
- Lines existing in the image may be detected as high-valued accumulator cells in the
accumulator array, and the parameters of the detected line are specified by the
accumulator array co-ordinates.
- As a result, line detection in the image is transformed to detection of local maxima in
the accumulator space.
- The parametric equation of the line y=kx+q is appropriate only for explanation
of the Hough transform principles -- it causes difficulties in vertical line
detection (k -> infinity) and in nonlinear discretization of the parameter
k.
- The following web site illustrates the discrete parameter space of the Hough
Transform and was created by Amos Storkey. The parameterization of the
lines used in this demonstration are given by the polar form of a line (see
Eq. 5.26). The movie can be downloaded here.
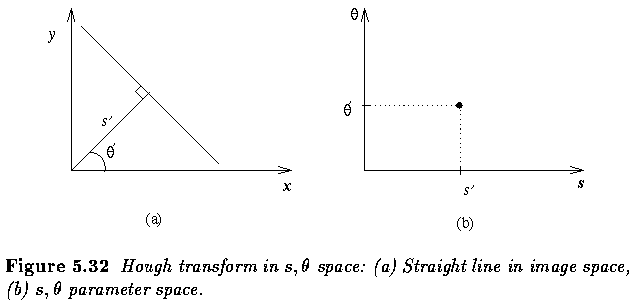
- If a line is represented as

the Hough transform does not suffer from these limitations.
- Again, the straight line is transformed to a single point
- The following web
site illustrates the sinusoidal curves in the Hough Transform Space produced
by the polar parameterization of a line. This web site was created by Rudy
Bock.
- Discretization of the parameter space is an important part of this approach.
- Also, detecting the local maxima in the accumulator array is a non-trivial problem.
- In reality, the resulting discrete parameter space usually has more than one local
maximum per line existing in the image, and smoothing the discrete parameter space may be
a solution.
- Generalization to more complex curves that can be described by an analytic equation is
straightforward.
- Consider an arbitrary curve represented by an equation f(x,a)=0, where {a} is the vector
of curve parameters.


- If we are looking for circles, the analytic expression f(x,a) of the desired curve is
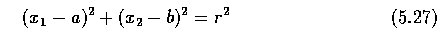
- where the circle has center (a,b) and radius r.
- Therefore, the accumulator data structure must be three-dimensional.
- Even though the Hough transform is a very powerful technique for curve detection,
exponential growth of the accumulator data structure with the increase of the number of
curve parameters restricts its practical usability to curves with few parameters.
- If prior information about edge directions is used, computational demands can be
decreased significantly.
- Consider the case of searching the circular boundary of a dark region, letting the
circle have a constant radius r=R for simplicity.
- Without using edge direction information, all accumulator cells A(a,b) are incremented
in the parameter space if the corresponding point (a,b) is on a circle with center x.
- With knowledge of direction, only a small number of the accumulator cells need be
incremented. For example, if edge directions are quantized into 8 possible values, only
one eighth of the circle need take part in incrementing of accumulator cells.
- Using edge directions, candidates for parameters a and b can be identified from the
following formulae:
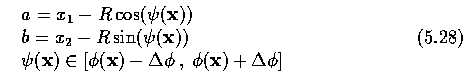
- where phi(x) refers to the edge direction in pixel x and Delta phi is the maximum
anticipated edge direction error.
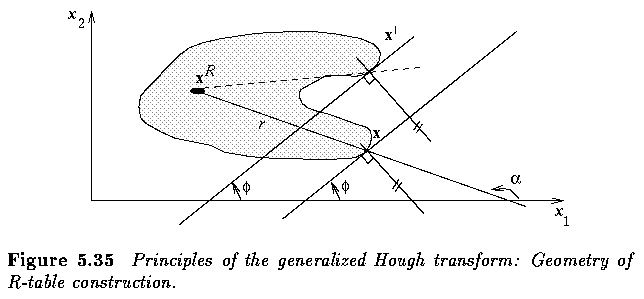
- Another heuristic that has a beneficial influence on the curve search is to weight the
contributions to accumulator cells A(a) by the edge magnitude in pixel x
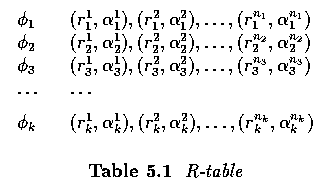


Border detection using border location
information
Region construction from borders

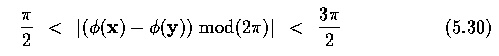
Last Modified: October 27, 2003
![[Go Back]](../IMAGES/next.gif)







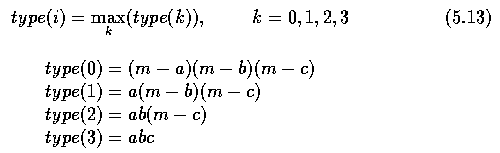
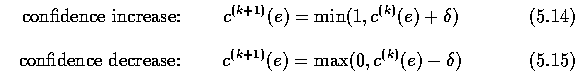
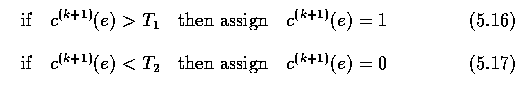






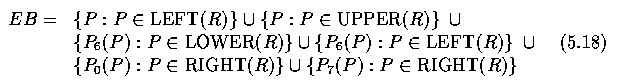








![]()
![]()
![]()
![]()











![]()



![]()