This page is provided for students who wish to print a copy of the transcript of this entire lesson.
Click here to return to the online version of Lesson 2.
In this lesson, we will cover the general topics of units and dimensions. The lesson will be organized in the following manner:
I realize that much of the material on this lesson will not be new to you since you have probably learned about units and dimensions in several other courses in your freshman year and in high school, and have been using them in everyday life since you could talk! However, this lesson will provide an important foundation for the rest of the course since units and dimensions play a pivotal role in how engineers communicate technical results to one another. Indeed, the ability to perform unit conversions is an essential skill for all engineers (and besides, most students benefit from repeated exposure to this topic).
To prepare for this lesson, I recommend that you read Chapter 2, sections 2.1 through 2.6 (pages 9 - 22) in the text (Elementary Principles of Chemical Processes, 2nd edition, by R.M. Felder and R.W. Rousseau).
Basic definitions:
A dimension is something that can be measured or quantified. Prominent examples of simple dimensions (those that cannot be derived by multiplying or dividing other dimensions) are length, time, mass, quantity, and temperature. Derived dimensions arise from multiplying or dividing other dimensions. Examples include volume (length3), velocity (length/time), density (mass/volume), and concentration (quantity/volume).
A unit is a standard magnitude of a given dimension against which other magnitudes of that dimension can be compared. For any given dimension, there are a host of different units that can be used to express a quantitative value. For example, units of length include inches, feet, meters, Angstroms, and light years, to name a few.
Three types of units have been identified: base units, multiple units, and derived units.
A base unit is a unit for a simple dimension that cannot be subdivided. These simple dimensions include length, time, mass, temperature, electric current, and light intensity.
A multiple unit is defined as a multiple or a fraction of a base unit. For example, the base unit for time is the second in all three of the systems of units discussed below. Examples of multiple units for time include minutes, hours, days, milliseconds, microseconds, etc.
A derived unit is defined by multiplying or dividing base units and multiple units. An engineer will use literally hundreds of derived units during the course of her career. For example, all units for force are derived units. A Newton is defined as a kg m /s2, and a dyne is defined as a g cm/s2 (weíll talk more about derived units for force later). Other derived units that will be important in this course include the units for velocity, acceleration, flow rate, concentration, composition, energy, density, heat capacity, pressure, work, and volume, to name just a few.
Systems of Units:
Periodically, attempts are made to establish standard systems of units that can be adopted widely throughout the world. Currently there are three systems that are commonly used in this country: the American engineering system, the CGS system, and the SI system (SI stands for Systeme Internationale).
The American Engineering system of units is based largely upon the English system of units that was adopted when the Magna Carta was signed in 1215. The base units for this system are the foot, the lbm, the second, and the Fahrenheit scale for length, mass, time, and temperature, respectively.
The CGS (centimeter-gram-second) system was devised in 1790 by the National Assembly of France in an attempt to establish a broadly accepted system of units since the English system was not widely adopted outside of the British empire (the Royal Society of London was invited to participate in devising the new system, but declined the invitation). The based units for this system are centimeter (length), gram (mass), second (time), mole (amount) and Kelvin (temperature).
The SI system was developed in the last attempt (in 1960) to establish a universal system of units by "cleaning up" some problems and confusions with the CGS system. For example, the CGS system used the unit of calorie for energy (the amount of energy needed to raise the temperature of one gram of water by one Celsius degree) rather than defining it as a derived unit in terms of other base units. Therefore the SI system adopted the Joule (kg m2/s2) as the unit for energy. The base units in the SI system are meter (length), kilogram (mass), second (time), mole (amount), and Kelvin (temperature).
Prefixes for Multiple Units
The choice of which multiple unit to use when expressing the measured value of a dimension is based primarily on the magnitude of the number to be expressed. People generally prefer to work with numerical values between 0.1 and 1000 (for example, you wouldnít express the distance from New York to Chicago in inches, or the volume of your carís gas tank in fluid ounces). One problem with the American engineering system of units is the peculiar set of conversion factors between multiple units (for example, 12 inches in a foot, 3 feet in a yard, 5280 feet in a mile, etc). In the SI and CGS systems, multiple units are conveniently expressed using standard prefixes that correspond to certain factors of 10. A table of these prefixes is given below:
| Prefix |
|
Factor |
| tera |
|
1012 |
| giga |
|
109 |
| mega |
|
106 |
| kilo |
|
103 |
| deci |
|
10-1 |
| centi |
|
10-2 |
| milli |
|
10-3 |
| micro |
|
10-6 |
| nano |
|
10-9 |
| pico |
|
10-12 |
| femto |
|
10-15 |
Unit Conversions
It is now clear that there are a wide variety of units that could be used to express a measured value. In fact, a measured value can be expressed in terms of any unit having the appropriate dimension. Conversion factors are used to convert a measured value from one unit to another. A conversion factor is simply a ratio of the equivalent number of one unit to the other unit.
Examples of conversion factors that you have become very familiar with may be used to convert between units within the same system of units:
![]()
Some examples of conversion factors between two different systems of units are:
![]()
The inside front cover of your text contains most of the common conversion factors you will need for this class.
To convert a measured value from one simple unit to another, you simply multiply by the appropriate conversion factor as shown below:
165 lbm (0.453593 kg / lbm) = 74.8 kg
To convert a measured value from one derived unit to another, you may have to multiply by a series of conversion factors as illustrated below:
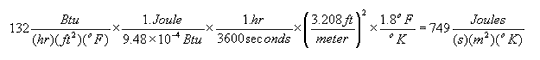
Units for Countable Objects
One dimension that is often confusing for students is the dimension that describes the quantity of discrete (countable) objects. These are items that always occur in integer quantities. Examples of such objects would include living beings (people, cows, cats, etc), mechanical devices such as cars, and items such as pieces of paper and molecules. Note that countable objects may have attributes that are measurable. For example, the people in a class are countable, but the weight of each person is measurable. Units that are available to describe the number of countable objects include a dozen (12 items), a gross (144 objects), and a mole (6.23 x 1023 objects).
Force, Mass, and Weight
Newtonís second law of motion states that the force exerted on an object is proportional to the mass of the object times the acceleration produced by the force. In the SI system of units, the proportionality constant is unity if the applied force is expressed in Newtons, the mass is expressed in kilograms, and the acceleration is expressed in meters per second per second. This convenient proportionality constant of unity occurs because a Newton is a derived unit that is defined to be equal to 1 kg . m/s2 (indeed, if a one Newton force were applied to a 1 kg mass it would result in an acceleration of 1 m/s2). For this reason, you are probably familiar with the following equation from high school physics:
F = m . a
The situation is a little more complicated for the American Engineering system of units. In this system, the unit of force is pound-force (lbf) and the preferred unit of mass is pound-mass (lbm). If a force of 1.0 lbf is applied to a mass of 1 lbm, the resulting acceleration is not 1 ft/s2, but is 32.174 ft/s2 (the acceleration of gravity at sea level and 45o latitude). For this reason, the proportionality constant between force and the product of mass and acceleration is not unity for the American engineering system of units. We will let the symbol gc represent the reciprocal of this proportionality constant; therefore Newtonís second law may be written as follows:
F = m . a/gc
The quantity gc is best viewed as a conversion factor between two different units for force as shown below:
Note that the slug is an alternative unit of mass in the American engineering systems of units. A slug is a larger mass than a lbm, and a force of 1 lbf will accelerate a slug at a rate of 1 ft/s2.
A related concept that can be very confusing (especially in the American Engineering system of units) is the relationship between mass and weight. Mass and weight are not the same thing, in fact, they have completely different dimensions. Mass is a simple dimension that characterizes the amount of matter making up an object. In contrast, weight has dimensions of force, which you will recall is a derived dimension equal to mass times acceleration. Indeed, weight is the force exerted on an object by gravitational attraction.
The weight of an object can be determined using Newtonís second law, as shown below:
W = m . g/gc
Here W represents the weight of the object of mass m, and g represents the acceleration of gravity (9.81 m/s2 or 32.174 ft/s2). Based upon this equation, it is easy to see that the weight of a 1 kg mass is 9.81 N, and the weight of 1 lbm is 1 lbf. The reason for the rather confusing convention for force and weight in the American engineering system ultimately arises from the fact that the original English system of units was adopted before Newtonís discovery of the second law of motion. Therefore, the English unit for mass was actually derived from the pre-existing unit of weight, and they were given the same name.
A second aspect of weight and mass in the American engineering system that is often confusing for students is the relationship between g and gc. Students typically think that gc is not needed for the SI or CGS systems (because it has a value of unity in these systems), and that g and gc are the same thing in the American engineering systems. This is not the case. The quantity g is the acceleration of gravity. Its value changes slightly as you change elevation on Earth, and would change dramatically if you were to travel to the moon or to a different planet (for example, g has a value of 5.36 ft/s2 on the moon, and 38.6 ft/s2 on Saturn). In contrast, quantity gc is a constant conversion factor. Its value does not change as you change locations ñ it has the same value on the moon as it does on Earth (however 1 lbm will not weigh 1 lbf on the moon, but will weight approximately one sixth of a lbf).
Temperature
The American engineering system of units uses the Fahrenheit temperature scale, which is named after Gabriel Fahrenheit, a German glass blower who made mercury thermometers and developed this temperature scale in the early 1700s. Fahrenheit assigned the value of zero temperature to the coldest freezing point that he could easily duplicate in his laboratory: the eutectic freezing point of a mixture of water and ammonium chloride. The highest possible temperature that he could record using his thermometers was the temperature at which the mercury started to boil, which he arbitrarily assigned to be 600 degrees. The magnitude of a Fahrenheit degree was then established by dividing the distance between these two temperatures into 600 equally spaced intervals.
An alternative temperature scale was established by a Swedish astronomer named Anders Celsius. He established the Celsius (or centigrade) scale by assigning the value of zero to the triple point of water (a temperature that is very easy to duplicate in the laboratory) and the value of 100 to the boiling point of water. The magnitude of the Celsius degree was then established by dividing the distance between these two temperatures into 100 equally spaced intervals.
Based upon these two scales, the Fahrenheit degree corresponds to a smaller temperature change than a Celsius degree (in fact, there are 1.8 Fahrenheit degrees in each Celsius degree). Therefore, to convert a temperature change from one scale to another, the conversion factor is given below:
To convert a temperature measurement from one scale to another, the following equation can be used:
T(oF) = 1.8T(oC) + 32
This equation is readily derived by noting that 0oC corresponds to 32oF, and that each one Celsius degree change in temperature corresponds to 1.8 Fahrenheit degrees.
Both the Fahrenheit and the Celsius temperature scales are relative scales rather than absolute scales since a temperature of zero does not correspond to a complete lack of temperature, and negative temperatures are possible. In contrast, all of the other dimensions that we have considered (length, time, mass, volume, etc) are based upon absolute scales since a value of zero corresponds to a complete lack of length, mass, time, volume, etc. In the 1700s the scientists could not imagine a complete lack of temperature, therefore the relative scales were adopted. In the years since the Fahrenheit and Celsius scales were devised, it has been recognized that temperature is really a measure of the average kinetic energy of the molecules making up the substance, and an absolute zero (corresponding to the lack of thermal motion) could be identified. This complete lack of thermal motion occurs at a temperature of -273.15 oC, and a temperature of ñ459.67 oF. Therefore, two absolute temperature scales have been adopted. The Kelvin and Rankine temperature scales are defined such that absolute zero is assigned the value of zero on the scales, with the size of the degree set equal to the Celsius degree (Kelvin scale) or the Fahrenheit degree (Rankine scale).
Therefore, the following three expressions can be used for conversions from one scale to another:
T(K) = T(oC) +273.15
T(oR) = T(oF) + 459.67
T(oR) = 1.8T(K)
Dimensional Homogeneity
An equation is said to be dimensionally homogeneous if all additive terms on both sides of the equation have the same dimensions. An example of a dimensionally homogeneous equation is the expression relating two pressures in a differential manometer used to measure the pressure difference for two points in a pipe. This equations is shown below:
![]()
|
Here; |
P1 |
is the pressure exerted on one side of the manometer (dimension of force/area); |
|
P2 |
is the pressure exerted on the other side on the manometer (dimension of force/area); |
|
|
rf |
is the density of the manometer fluid (dimension of mass/volume); |
|
|
r |
is the density of the fluid flowing in the pipe (dimension of mass/volume); |
|
|
h |
is the height of the manometer fluid on the low pressures side of the instrument relative to the height on the high pressure side (dimension of length) |
To test whether this equation is dimensionally homogeneous, we will multiply the equation out, then will examine the dimensions of each term:
The two terms on the left side of the equation obviously have dimensions of force/area, therefore, the equation is dimensionally homogeneous if the quantity (r.h.g/gc) also has these units.
r times h has dimensions of mass/area, and g/gc has dimensions of force/mass, therefore the term (r h g/gc) does indeed have the proper dimensions and the equation is dimensionally homogeneous.
An equation that is not dimensionally homogeneous cannot possibly be valid (in fact, it makes no sense).
An equation that is dimensionally homogeneous, but inconsistent in units, may be made consistent by multiplying by appropriate conversion factors.