Statistical convergence

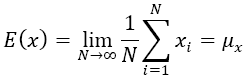
For a random variable x,

• Expected value of x,

• Sample mean of x,

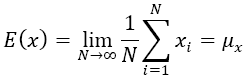
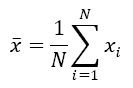
• Statistical convergence can be defined such as

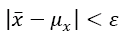
for any ε > 0.

Confidence interval, d

• For normal data

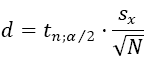
• For non-normal data with unknown distribution

Statistical Convergence Error

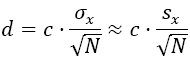
For a stationary random variable x,

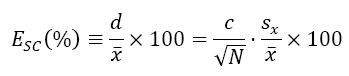
where, d is the confidence interval size, x is the sample mean, s_x is the standard deviation, and N is the number of data.

For a 95% confidence level:

If x is normal, c = 2.0 by using the Student-t statistics,

If x is not normal with unknown distribution, c = 4.5 by using the Tchebycheff inequality.

Stationarity

For a random process {x(t)}^*, mean value μ_x(t) and autocorrelation function R_x(t,t+τ) are given by

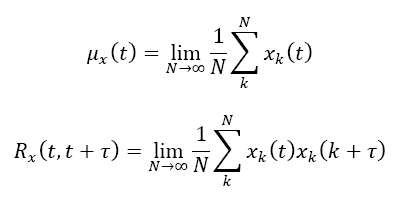
* the symbol { } is used to denote an ensemble of sample function.

Stationary:  μ_x(t) and R_x(t,t+τ) do not vary as time t varies, i.e., μ_x(t) = μ_x and R_x(t,t+τ) = R_x(τ).

• Weakly stationary

• Strongly stationary

Self-stationary: for the k^th same function, the sample properties μ_x(t,k) and R_x(t,t+τ,k) do not vary.