
57:020 Fluid Mechanics
28
Dimensional analysis
• Definition
: Dimensional analysis is a process of formulating
fluid mechanics problems in
in terms of
non-dimensional variables and parameters.
• Why is it used :
• Reduction in variables ( If F(A1, A2, … , An) = 0,
then f(P1, P2, … Pr < n) = 0,
where, F =
functional form, Ai = dimensional variables,
Pj = non-dimensional
parameters,
m = number of important dimensions, n = number of dimensional variables,
r
= n – m ).
Thereby the number of experiments required to determine f vs. F is
reduced.
• Helps in
understanding physics
• Useful in data
analysis and modeling
• Enables
scaling of different physical dimensions and fluid properties
Example
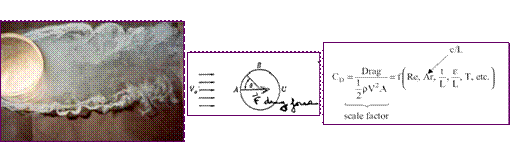
Vortex shedding behind cylinder
Drag = f(V, L, r, m, c, t, e, T, etc.)
From dimensional analysis,

Examples of dimensionless quantities : Reynolds number,
Froude
Number, Strouhal
number, Euler number, etc.