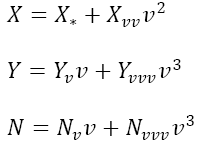
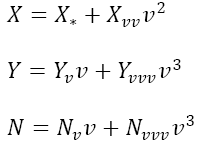
Hydrodynamic derivatives

1. Static drift

Sway velocity derivatives are determined by curve fitting the static drift test data measured over a range of drift angle β.

2. Dynamic tests

Hydrodynamic derivatives can be evaluated by using either the 'Multiple-Run' or 'Single-Run' method.

Hydrodynamic derivatives are evaluated by curve fitting the harmonics data obtained from a multiple number of dynamic PMM tests over a range of PMM motion parameters.

1) Sway derivatives

2) Yaw derivatives

3) Cross-coupled derivatives

'Single-Run' (SR) method:

Hydrodynamic derivatives are evaluated by solving the mathematic model equations using the harmonics data from a single number of dynamic PMM tests for a fixed PMM motion parameter value.

Ex) pure sway test:

1) Sway derivatives

2) Yaw derivatives

3) Cross-coupled derivatives

3. Surge derivatives

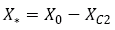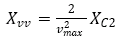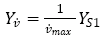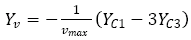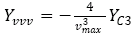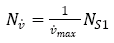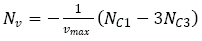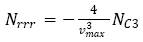Sway	Yaw

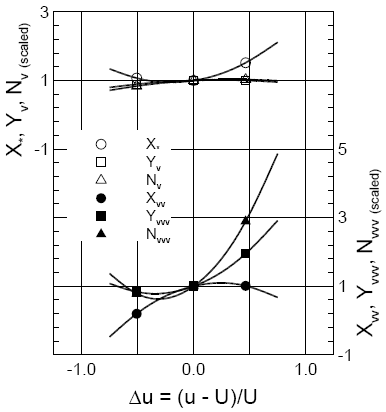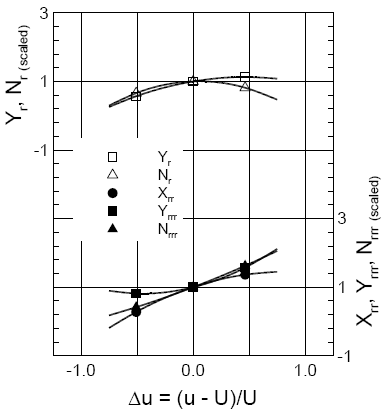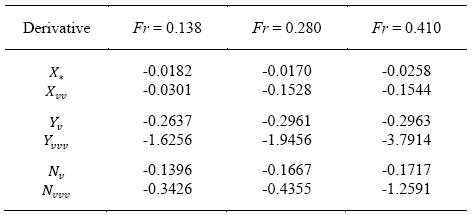
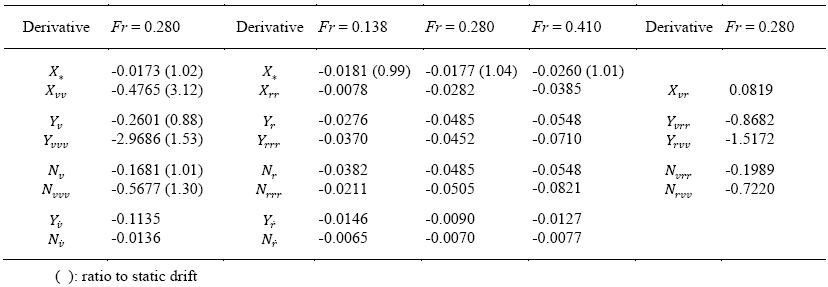
Note: 1) Derivatives are scaled (normalized) with the values at Fr = 0.280

2) Δu = -0.51, 0.0, 0.46 corresponds to Fr = 0.138, 0.280, 0.410, respectively.

4. Reconstruction Error

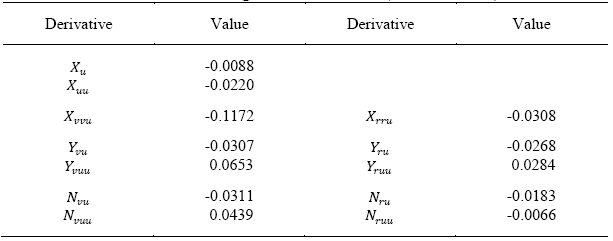
The validities of hydrodynamic derivatives determined using the MR and SR methods are evaluated by examining the errors in reconstruction of forces and moment data time-histories through the mathematic model.
Reconstruction error is defined as

where

D_i is the measured data

R_i is the reconstructed data

1) Sway derivatives reconstructing the pure sway time histories:

2) Yaw derivatives reconstructing the pure yaw time histories:

3) Cross-coupled derivatives reconstructing the yaw and drift time histories:

Summary:

For MR method, the reconstruction error in general E_R (%) < 20 over the entire range of the tested PMM parameters.
For SR method, the error value is typically huge, E_R (%) < 600, when PMM motion is small, and relatively large, E_R (%) < 50, as the PMM motion becomes large.
Consequently, the MR method is more rigorous than the SR method, and the SR method is only suggested when PMM motion is large enough.