- Jessica Young, an UI student, considers herself an average cigarette smoker, for she consumes about a carton a week. She wonders how much money she could accumulate by the time she reaches 60 if she quit smoking now and put her cigarette money into a saving account. Cigarettes cost $10 per carton. Ron expects that a savings account would earn 6% interest, compounded semi-annually. Compute Jessica's future worth at age 60. (Jessica is now 20 yrs old) (10 points)
Solution: Semi-annual saving $10/carton x 26 weeks = $260 FW = A(F/A,3%, 80) = 260 x 321.363 = 83,554.38 - A firm is trying to decide which of two devices to install to reduce costs in a particular situation. Both devices cost $1000 and have useful lives of 5 years and no salvage value. Device A can be expected to result in $300 savings annually. Device B will provide cost savings of $500 the first year, but will decline $50 annually, making the second-year savings $450, the third-year savings $400, and so forth. With interest at 6%, which device should the firm purchase? (Use benefit/Cost ratio to solve this problem) (20 point)
- PW of cost = $1000
PW of benefits = 300(P/A, 6%, 5) = 300x4.212 = 1263.6 B/C ratio = 1.263 - PW of cost = $1000
PW of benefits = 500(P/A, 6%, 5) - 50(P/G, 6%,5) = 500x4.212 - 50 x 7.934 = 1709.3 B/C ratio = 1.709
- Consider the three mutually exclusive alternatives below. Each alternative has a 10-year life and no salvage value. If the minimum attractive rate or return is 5%, which alternative should be selected? (20 points)
| | A | B | C | | Initial cost | $2000 | $4000 | $6000 | | Uniform | 400 | 650 | 700 |
- Complete the following Benefit-cost graph
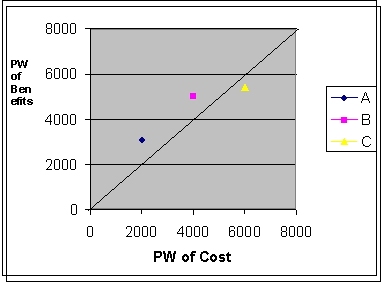
A: PW Benefits = 400(P/A, 10, 5%) = 400 x 7.722 = 3089 B: PW Benefits = 650(P/A, 10, 5%) = 5019 C: PW Benefits =700(P/A,10,5%) = 5405 - Based on this graph, which alternative should be selected? Why?
C has a B/C ratio less than 1, C is out Consider Upgrade from A to B, The incremental B/C ratio (the slop of line AB ) = (5019-3089)/(4000-2000) is less than 1, should still go with A. - Suppose B is the preferred at its current initial cost of $4000, how much higher than $4000 can the initial cost be and still have B the preferred alternative?
NPW of alternative A = 3089 - 2000 = 1089 NPW of alternative B = 5019 -x NPW of alternative C = 5405 - 6000 = -595** ç Since it is negative, you should never upgrade from B to C, as a result you don't spend any money more than $4000 to upgrade B to C. Sorry this question is very confusing.) |
![]()