55:148 Digital Image Processing
Chapter 4, Part II
Image Pre-processing: Geometric transformations
Related Reading
Sections from Chapter 4 according to the WWW Syllabus.
Chapter 4.2 Overview:
Geometric transformations
- Geometric transforms permit the elimination of geometric distortion that occurs when an
image is captured.
- An example is an attempt to match remotely sensed images of the same area taken after
one year, when the more recent image was probably not taken from precisely the same
position.
- To inspect changes over the year, it is necessary first to execute a geometric
transformation, and then subtract one image from the other.
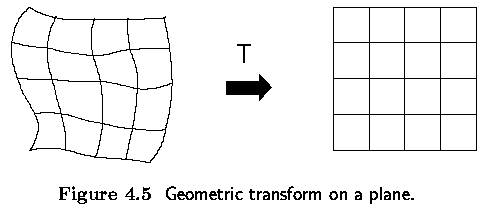
- A geometric transform is a vector function T that maps the pixel (x,y) to a new position
(x',y').

- The transformation equations are either known in advance or can be determined from known
original and transformed images.
- Several pixels in both images with known correspondence are used to derive the unknown
transformation.
- A geometric transform consists of two basic steps ...
- 1. determining the pixel co-ordinate transformation
- mapping of the co-ordinates of the input image pixel to the point in the output image.
- the output point co-ordinates should be computed as continuous values (real numbers) as
the position does not necessarily match the digital grid after the transform.
- 2. finding the point in the digital raster which matches the transformed point and
determining its brightness.
- brightness is usually computed as an interpolation of the brightnesses of several points
in the neighborhood.
Pixel co-ordinate transformations
- General case of finding the co-ordinates of a point in the output image after a
geometric transform.
- usually approximated by a polynomial equation

- This transform is linear with respect to the coefficients ark, brk
- If pairs of corresponding points (x,y), (x',y') in both images are known, it is possible
to determine ark, brk by solving a set of linear equations.
- More points than coefficients are usually used to get robustness.
- If the geometric transform does not change rapidly depending on position in the image,
low order approximating polynomials, m=2 or m=3, are used, needing at least 6 or 10 pairs
of corresponding points.
- The corresponding points should be distributed in the image in a way that can express
the geometric transformation - usually they are spread uniformly.
- The higher the degree of the approximating polynomial, the more sensitive to the
distribution of the pairs of corresponding points the geometric transform.
- In practice, the geometric transform is often approximated by the bilinear
transformation
- 4 pairs of corresponding points are sufficient to find transformation coefficients

- Even simpler is the affine transformation for which three pairs of corresponding
points are sufficient to find the coefficients

- The affine transformation includes typical geometric transformations such as
- rotation, translation, scaling and skewing.
Practical Experiment 4.C - VIP Version
Practical Experiment 4.C - Khoros Version
- Open Warp-example.wksp located in the ~dip/examples/khoros.dir directory
- Perform several geometric transforms by modifying the warping coefficients
- Perform translation, scaling, and skewing
- A geometric transform applied to the whole image may change the co-ordinate system, and
a Jacobean J provides information about how the co-ordinate system changes

- If the transformation is singular (has no inverse) then J=0. If the area of the image is
invariant under the transformation then J=1.
- The Jacobean for the general bilinear transform (4.11)

- The Jacobean for the affine transformation (4.12)

- Important geometric transformations
- Rotation - by the angle phi about the origin

- Change of scale - a in the x axis and b in the y axis


- Complex geometric transformations (distortion)
- approximation by partitioning an image into smaller rectangular subimages;
- for each subimage, a simple geometric transformation, such as the affine, is estimated
using pairs of corresponding pixels.
- geometric transformation (distortion) is then performed separately in each subimage.
- Typical geometric distortions which have to be overcome in remote sensing:
- distortion of the optical systems
- nonlinearities in row by row scanning
- nonconstant sampling period.
Brightness interpolation
- Assume that the planar transformation has been accomplished, and new point co-ordinates
(x',y') were obtained.
- The position of the point does not in general fit the discrete raster of the output
image.
- Values on the integer grid are needed.
- Each pixel value in the output image raster can be obtained by brightness
interpolation of some neighboring noninteger samples.
- The brightness interpolation problem is usually expressed in a dual way (by determining
the brightness of the original point in the input image that corresponds to the point in
the output image lying on the discrete raster).
- Computing the brightness value of the pixel (x',y') in the output image where x' and y'
lie on the discrete raster

- In general the real co-ordinates after inverse transformation (dashed lines in Figures)
do not fit the input image discrete raster (solid lines), and so brightness is not known.
- To get the brightness value of the point (x,y) the input image is resampled.

- f_{n}(x,y) ... result of interpolation
- h_{n} is the interpolation kernel
- Usually, a small neighborhood is used, outside which h_{n} is zero.
Nearest neighbor interpolation
- assigns to the point (x,y) the brightness value of the nearest point g in the discrete
raster

- The right side of Figure shows how the new brightness is assigned.
- Dashed lines show how the inverse planar transformation maps the raster of the output
image into the input image - full lines show the raster of the input image.

- The position error of the nearest neighborhood interpolation is at most half a pixel.
- This error is perceptible on objects with straight line boundaries that may appear
step-like after the transformation.
Linear interpolation
- explores four points neighboring the point (x,y), and assumes that the brightness
function is linear in this neighborhood.

- Linear interpolation is given by the equation

- Linear interpolation can cause a small decrease in resolution and blurring due to its
averaging nature.
- The problem of step like straight boundaries with the nearest neighborhood interpolation
is reduced.
Bicubic interpolation
- improves the model of the brightness function by approximating it locally by a bicubic
polynomial surface; sixteen neighboring points are used for interpolation.
- interpolation kernel (`Mexican hat') is given by

- Bicubic interpolation does not suffer from the step-like boundary problem of nearest
neighborhood interpolation, and copes with linear interpolation blurring as well.
- Bicubic interpolation is often used in raster displays that enable zooming with respect
to an arbitrary point -- if the nearest neighborhood method were used, areas of the same
brightness would increase.
- Bicubic interpolation preserves fine details in the image very well.
[Back one section]
[Table of Contents]
[Next Section]
Last Modified: September 8, 2003
![[Go Back]](../IMAGES/next.gif)


![]()




![]()
![]()



![]()

![]()



