Copyright © 1997-02-27 (c)
This document clarifies aspects of colour specification and image coding that are important to computer graphics, image processing, video, and the transfer of digital images to print.
I assume that you are familiar with intensity, luminance (CIE Y), lightness (CIE L*), and the nonlinear relationship between CRT voltage and intensity (gamma). To learn more about these topics, read the companion Frequently Asked Questions about Gamma.
I retain copyright to this note. You have permission to use it, but you may not publish it.
Another source of information concerning color is the document Frequently asked questions about Colour Physics, by Steve Westland <coa23@cc.keele.ac.uk>.
If you have an Acrobat Reader, or if you would like to print this document, I recommend that you obtain the Acrobat PDF version (277356 bytes) of this note. You can find information about document formats.
I retain copyright to this note. You have permission to use it, but you may not publish it.
The human retina has three types of colour photoreceptor cone cells, which respond to incident radiation with somewhat different spectral response curves. A fourth type of photoreceptor cell, the rod, is also present in the retina. Rods are effective only at extremely low light levels (colloquially, night vision), and although important for vision play no role in image reproduction.
Because there are exactly three types of colour photoreceptor, three numerical components are necessary and sufficient to describe a colour, providing that appropriate spectral weighting functions are used. This is the concern of the science of colorimetry. In 1931, the Commission Internationale de L'Éclairage (CIE) adopted standard curves for a hypothetical Standard Observer. These curves specify how an SPD can be transformed into a set of three numbers that specifies a colour.
The CIE system is immediately and almost universally applicable to self-luminous sources and displays. However the colours produced by reflective systems such as photography, printing or paint are a function not only of the colourants but also of the SPD of the ambient illumination. If your application has a strong dependence upon the spectrum of the illuminant, you may have to resort to spectral matching.
Sir Isaac Newton said, "Indeed rays, properly expressed, are not coloured." SPDs exist in the physical world, but colour exists only in the eye and the brain.
The voltages presented to a CRT monitor control the intensities of the colour components, but in a nonlinear manner. CRT voltages are not proportional to intensity.
The magnitude of luminance is proportional to physical power. In that sense it is like intensity. But the spectral composition of luminance is related to the brightness sensitivity of human vision.
Strictly speaking, luminance should be expressed in a unit such as candelas per meter squared, but in practice it is often normalized to 1 or 100 units with respect to the luminance of a specified or implied white reference. For example, a studio broadcast monitor has a white reference whose luminance is about 80 cd*m -2, and Y = 1 refers to this value.

Yn is the luminance of the white reference. If you normalize luminance to reference white then you need not compute the fraction. The CIE definition applies a linear segment with a slope of 903.3 near black, for (Y/Yn) <= 0.008856. The linear segment is unimportant for practical purposes but if you don't use it, make sure that you limit L* at zero. L* has a range of 0 to 100, and a "delta L-star" of unity is taken to be roughly the threshold of visibility.
Stated differently, lightness perception is roughly logarithmic. An observer can detect an intensity difference between two patches when their intensities differ by more than one about percent.
Video systems approximate the lightness response of vision using R'G'B' signals that are each subject to a 0.45 power function. This is comparable to the 1/3 power function defined by L*.
The systems useful today for colour specification include CIE XYZ, CIE xyY, CIE L*u*v* and CIE L*a*b*. Numerical values of hue and saturation are not very useful for colour specification, for reasons to be discussed in section 36.
A colour specification system needs to be able to represent any colour with high precision. Since few colours are handled at a time, a specification system can be computationally complex. Any system for colour specification must be intimately related to the CIE specifications.
You can specify a single "spot" colour using a colour order system such as Munsell. Systems like Munsell come with swatch books to enable visual colour matches, and have documented methods of transforming between coordinates in the system and CIE values. Systems like Munsell are not useful for image data. You can specify an ink colour by specifying the proportions of standard (or secret) inks that can be mixed to make the colour. That's how PANTONE[tm] works. although widespread, it's proprietary. No translation to CIE is publicly available.
In theory, the three numerical values for image coding could be provided by a colour specification system. But a practical image coding system needs to be computationally efficient, cannot afford unlimited precision, need not be intimately related to the CIE system and generally needs to cover only a reasonably wide range of colours and not all of the colours. So image coding uses different systems than colour specification.
The systems useful for image coding are linear RGB, nonlinear R'G'B', nonlinear CMY, nonlinear CMYK, and derivatives of nonlinear R'G'B' such as Y'CBCR. Numerical values of hue and saturation are not useful in colour image coding.
If you manufacture cars, you have to match the colour of paint on the door with the colour of paint on the fender. A colour specification system will be necessary. But to convey a picture of the car, you need image coding. You can afford to do quite a bit of computation in the first case because you have only two coloured elements, the door and the fender. In the second case, the colour coding must be quite efficient because you may have a million coloured elements or more.
For a highly readable short introduction to colour image coding, see DeMarsh and Giorgianni [2]. For a terse, complete technical treatment, read Schreiber [3].
If three sources appear red, green and blue, and have the same radiance in the visible spectrum, then the green will appear the brightest of the three because the luminous efficiency function peaks in the green region of the spectrum. The red will appear less bright, and the blue will be the darkest of the three. As a consequence of the luminous efficiency function, all saturated blue colours are quite dark and all saturated yellows are quite light. If luminance is computed from red, green and blue, the coefficients will be a function of the particular red, green and blue spectral weighting functions employed, but the green coefficient will be quite large, the red will have an intermediate value, and the blue coefficient will be the smallest of the three.
Contemporary CRT phosphors are standardized in Rec. 709 [8], to be described in section 17. The weights to compute true CIE luminance from linear red, green and blue (indicated without prime symbols), for the Rec. 709, are these:
![]()
This computation assumes that the luminance spectral weighting can be formed as a linear combination of the scanner curves, and assumes that the component signals represent linear-light. Either or both of these conditions can be relaxed to some extent depending on the application.
Some computer systems have computed brightness using (R+G+B)/3. This is at odds with the properties of human vision, as will be discussed under What are HSB and HLS? in section 36.
The coefficients 0.299, 0.587 and 0.114 properly computed luminance for monitors having phosphors that were contemporary at the introduction of NTSC television in 1953. They are still appropriate for computing video luma to be discussed below in section 11. However, these coefficients do not accurately compute luminance for contemporary monitors.
There are practical reasons in video to perform these operations in the opposite order. First a nonlinear transfer function - gamma correction - is applied to each of the linear R, G and B. Then a weighted sum of the nonlinear components is computed to form a signal representative of luminance. The resulting component is related to brightness but is not CIE luminance. Many video engineers call it luma and give it the symbol Y'. It is often carelessly called luminance and given the symbol Y. You must be careful to determine whether a particular author assigns a linear or nonlinear interpretation to the term luminance and the symbol Y.
The coefficients that correspond to the "NTSC" red, green and blue CRT phosphors of 1953 are standardized in ITU-R Recommendation BT. 601-2 (formerly CCIR Rec. 601-2). I call it Rec. 601. To compute nonlinear video luma from nonlinear red, green and blue:
![]()
The prime symbols in this equation, and in those to follow, denote nonlinear components.
The magnitudes of the XYZ components are proportional to physical energy, but their spectral composition corresponds to the colour matching characteristics of human vision.
The CIE system is defined in Publication CIE No 15.2, Colorimetry, Second Edition (1986) [4].
If you place on your scanner an original coloured object that has "original" SPDs that are not already a record of three components, chances are your scanner will not very report accurate RGB values. This is because most scanners do not conform very closely to CIE standards.
![]()
A colour plots as a point in an (x, y) chromaticity diagram. When a narrowband SPD comprising power at just one wavelength is swept across the range 400 nm to 700 nm, it traces a shark-fin shaped spectral locus in (x, y) coordinates. The sensation of purple cannot be produced by a single wavelength: to produce purple requires a mixture of shortwave and longwave light. The line of purples on a chromaticity diagram joins extreme blue to extreme red. All colours are contained in the area in (x, y) bounded by the line of purples and the spectral locus.
A colour can be specified by its chromaticity and luminance, in the form of an xyY triple. To recover X and Z from chromaticities and luminance, use these relations:
![]()
The bible of colour science is Wyszecki and Styles, Color Science [5]. But it's daunting. For Wyszecki's own condensed version, see Color in Business, Science and Industry, Third Edition [6]. It is directed to the colour industry: ink, paint and the like. For an approachable introduction to the same theory, accompanied by descriptions of image reproduction, try to find a copy of R.W.G. Hunt, The Reproduction of Colour [7]. But sorry to report, as I write this, it's out of print.
It is often convenient for purposes of calculation to define white as a uniform SPD. This white reference is known as the equal-energy illuminant, or CIE Illuminant E.
A more realistic reference that approximates daylight has been specified numerically by the CIE as Illuminant D65. You should use this unless you have a good reason to use something else. The print industry commonly uses D50 and photography commonly uses D55. These represent compromises between the conditions of indoor (tungsten) and daylight viewing.
Although an illuminant can be specified informally by its colour temperature, a more complete specification is provided by the chromaticity coordinates of the SPD of the source.
Modern blue CRT phosphors are more efficient with respect to human vision than red or green. In a quest for brightness at the expense of colour accuracy, it is common for a computer display to have excessive blue content, about twice as blue as daylight, with white at about 9300 K.
Human vision adapts to white in the viewing environment. An image viewed in isolation - such as a slide projected in a dark room - creates its own white reference, and a viewer will be quite tolerant of errors in the white point. But if the same image is viewed in the presence of an external white reference or a second image, then differences in white point can be objectionable.
Complete adaptation seems to be confined to the range 5000 K to 5500 K. For most people, D65 has a little hint of blue. Tungsten illumination, at about 3200 K, always appears somewhat yellow.
An additive RGB system is specified by the chromaticities of its primaries and its white point. The extent (gamut) of the colours that can be mixed from a given set of RGB primaries is given in the (x, y) chromaticity diagram by a triangle whose vertices are the chromaticities of the primaries.
In computing there are no standard primaries or white point. If you have an RGB image but have no information about its chromaticities, you cannot accurately reproduce the image.
The NTSC in 1953 specified a set of primaries that were representative of phosphors used in colour CRTs of that era. But phosphors changed over the years, primarily in response to market pressures for brighter receivers, and by the time of the first the videotape recorder the primaries in use were quite different than those "on the books". So although you may see the NTSC primary chromaticities documented, they are of no use today.
Contemporary studio monitors have slightly different standards in North America, Europe and Japan. But international agreement has been obtained on primaries for high definition television (HDTV), and these primaries are closely representative of contemporary monitors in studio video, computing and computer graphics. The primaries and the D65 white point of Rec. 709 [8] are:
R G B white x 0.640 0.300 0.150 0.3127 y 0.330 0.600 0.060 0.3290 z 0.030 0.100 0.790 0.3582For a discussion of nonlinear RGB in computer graphics, see Lindbloom [9]. For technical details on monitor calibration, consult Cowan [10].
Details can be found in SMPTE RP 177-1993 [11].
To transform from CIE XYZ into Rec. 709 RGB (with its D65 white point), use this transform:
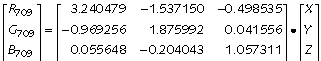
This matrix has some negative coefficients: XYZ colours that are out of gamut for a particular RGB transform to RGB where one or more RGB components is negative or greater than unity.
Here's the inverse transform. Because white is normalized to unity, the middle row sums to unity:
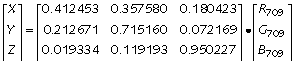
To recover primary chromaticities from such a matrix, compute little x and y for each RGB column vector. To recover the white point, transform RGB=[1, 1, 1] to XYZ, then compute x and y.
The importance of Rec. 709 as an interchange standard in studio video, broadcast television and high definition television, and the perceptual basis of the standard, assures that its parameters will be used even by devices such as flat-panel displays that do not have the same physics as CRTs.
As an example, here is the transform from SMPTE 240M (or SMPTE RP 145) RGB to Rec. 709:
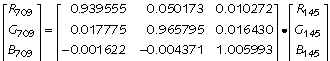
All of these terms are close to either zero or one. In a case like this, if the transform is computed in the nonlinear (gamma-corrected) R'G'B' domain the resulting errors will be insignificant.
Here's another example. To transform EBU 3213 RGB to Rec. 709:
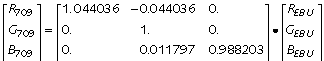
Transforming among RGB systems may lead to an out of gamut RGB result where one or more RGB components is negative or greater than unity.
In physical terms the spectral transmission curves of the colourants multiply, so this method of colour reproduction should really be called "multiplicative". Photographers and printers have for decades measured transmission in base-10 logarithmic density units, where transmission of unity corresponds to a density of 0, transmission of 0.1 corresponds to a density of 1, transmission of 0.01 corresponds to a density of 2 and so on. When a printer or photographer computes the effect of filters in tandem, he subtracts density values instead of multiplying transmission values, so he calls the system subtractive.
To achieve a wide range of colours in a subtractive system requires filters that appear coloured cyan, yellow and magenta (CMY). Cyan in tandem with magenta produces blue, cyan with yellow produces green, and magenta with yellow produces red. Smadar Nehab suggests this memory aid:
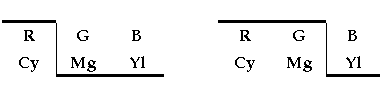
Additive primaries are at the top, subtractive at the bottom. On the left, magenta and yellow filters combine to produce red. On the right, red and green sources add to produce yellow.
Practical photographic dyes and offset printing inks have spectral absorption curves that overlap significantly. Most magenta dyes absorb mediumwave (green) light as expected, but incidentally absorb about half that amount of shortwave (blue) light. If reproduction of a colour, say brown, requires absorption of all shortwave light then the incidental absorption from the magenta dye is not noticed. But for other colours, the "one minus RGB" formula produces mixtures with much less blue than expected, and therefore produce pictures that have a yellow cast in the mid tones. Similar but less severe interactions are evident for the other pairs of practical inks and dyes.
Due to the spectral overlap among the colourants, converting CMY using the "one-minus-RGB" method works for applications such as business graphics where accurate colour need not be preserved, but the method fails to produce acceptable colour images.
Multiplicative mixture in a CMY system is mathematically nonlinear, and the effect of the unwanted absorptions cannot be easily analyzed or compensated. The colours that can be mixed from a particular set of CMY primaries cannot be determined from the colours of the primaries themselves, but are also a function of the colours of the sets of combinations of the primaries.
Print and photographic reproduction is also complicated by nonlinearities in the response of the three (or four) channels. In offset printing, the physical and optical processes of dot gain introduce nonlinearity that is roughly comparable to gamma correction in video. In a typical system used for print, a black code of 128 (on a scale of 0 to 255) produces a reflectance of about 0.26, not the 0.5 that you would expect from a linear system. Computations cannot be meaningfully performed on CMY components without taking nonlinearity into account.
For a detailed discussion of transferring colorimetric image data to print media, see Stone [15].
Other printing processes may or may not be subject to similar constraints.
In its second sense, colour difference refers to colour components where brightness is "removed". Vision has poor response to spatial detail in coloured areas of the same luminance, compared to its response to luminance spatial detail. If data capacity is at a premium it is advantageous to transmit luminance with full detail and to form two colour difference components each having no contribution from luminance. The two colour components can then have spatial detail removed by filtering, and can be transmitted with substantially less information capacity than luminance.
Instead of using a true luminance component to represent brightness, it is ubiquitous for practical reasons to use a luma signal that is computed nonlinearly as outlined above ( What is luma? ).
The easiest way to "remove" brightness information to form two colour channels is to subtract it. The luma component already contains a large fraction of the green information from the image, so it is standard to form the other two components by subtracting luma from nonlinear blue (to form B'-Y' ) and by subtracting luma from nonlinear red (to form R'-Y' ). These are called chroma.
Various scale factors are applied to (B'-Y' ) and (R'-Y' ) for different applications. The Y 'PBPR scale factors are optimized for component analog video. The Y 'CBCR scaling is appropriate for component digital video such as studio video, JPEG and MPEG. Kodak's PhotoYCC[tm] uses scale factors optimized for the gamut of film colours. Y'UV scaling is appropriate as an intermediate step in the formation of composite NTSC or PAL video signals, but is not appropriate when the components are kept separate. The Y 'UV nomenclature is now used rather loosely, and it sometimes denotes any scaling of (B'-Y' ) and (R'-Y' ). Y 'IQ coding is obsolete.
The subscripts in CBCR and PBPR are often written in lower case. I find this to compromise readability, so without introducing any ambiguity I write them in uppercase. Authors with great attention to detail sometimes "prime" these quantities to indicate their nonlinear nature, but because no practical image coding system employs linear colour differences I consider it safe to omit the primes.
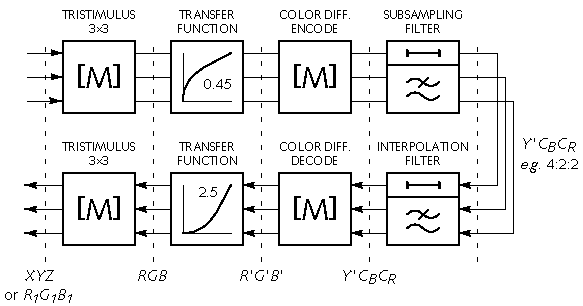
From linear XYZ - or linear R1 G1 B1 whose chromaticity coordinates are different from the interchange standard - apply a 3 x 3 matrix transform to obtain linear RGB according to the interchange primaries. Apply a nonlinear transfer function ("gamma correction") to each of the components to get nonlinear R'G'B'. Apply a 3 x 3 matrix to obtain colour difference components such as Y'PBPR , Y'CBCR or PhotoYCC. If necessary, apply a colour subsampling filter to obtain subsampled colour difference components. To decode, invert the above procedure: run through the block diagram right-to-left using the inverse operations. If your monitor conforms to the interchange primaries, decoding need not explicitly use a transfer function or the tristimulus 3 x 3.
The block diagram emphasizes that 3 x 3 matrix transforms are used for two distinctly different tasks. When someone hands you a 3 x 3, you have to ask for which task it is intended.
To encode Y'PBPR , start with the basic Y', (B'-Y' ) and (R'-Y' ) relationships:
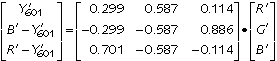
Y'PBPR components have unity excursion, where Y' ranges [0..+1] and
each of PB and PR ranges [-0.5..+0.5]. The (B'-Y' ) and (R'-Y'
) rows need to be scaled by ![]() and
and ![]() . To
encode from R'G'B' where reference black is 0 and reference white is +1:
. To
encode from R'G'B' where reference black is 0 and reference white is +1:
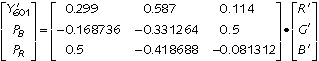
The first row comprises the luma coefficients; these sum to unity. The second and third rows each sum to zero, a necessity for colour difference components. The +0.5 entries reflect the maximum excursion of PB and PR of +0.5, for the blue and red primaries [0, 0, 1] and [1, 0, 0].
The inverse, decoding matrix is this:
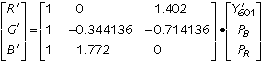
To compute Y'CBCR from R'G'B' in the range [0..+1], scale the rows of the matrix of Eq 2 by the factors 219, 224 and 224, corresponding to the excursions of each of the components:
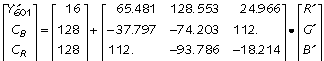
Summing the first row of the matrix yields 219, the luma excursion from black to white. The two entries of 112 reflect the positive CBCR extrema of the blue and red primaries.
Clamp all three components to the range 1 through 254 inclusive, since Rec. 601 reserves codes 0 and 255 for synchronization signals.
To recover R'G'B' in the range [0..+1] from Y'CBCR, use the inverse of Eq 3 above:
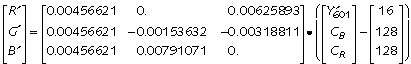
This looks overwhelming, but the Y'CBCR components are integers in eight bits and the reconstructed R'G'B' are scaled down to the range [0..+1].
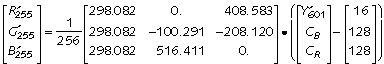
To decode R'G'B' in the range [0..255] from Rec. 601 Y'CBCR, using eight-bit binary arithmetic:
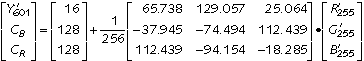
The multiplications by 1/256 can be accomplished by shifting. Some of the coefficients, when scaled by 1/256, are larger than unity. These coefficients will need more than eight multiplier bits.
For implementation in binary arithmetic the matrix coefficients have to be rounded. When you round, take care to preserve the row sums of [1, 0, 0].
The matrix of Eq 4 will decode standard Y'CBCR components to RGB components in the range [0..255], subject to roundoff error. You must take care to avoid overflow due to roundoff error. But you must protect against overflow in any case, because studio video signals use the extremes of the coding range to handle signal overshoot and undershoot, and these will require clipping when decoded to an RGB range that has no headroom or footroom.
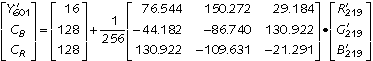
To decode R'G'B' in the range [0..219] from Y'CBCR, using eight-bit binary arithmetic:
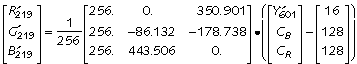
The entries of 256 in this matrix indicate that the corresponding component can simply be added; there is no need for a multiplication operation. This matrix contains entries larger than 256; the corresponding multipliers will need capability for nine bits.
The matrices in this section conform to Rec. 601 and apply directly to conventional 525/59.94 and 625/50 video. It is not yet decided whether emerging HDTV standards will use the same matrices, or adopt a new set of matrices having different luma coefficients. In my view it would be unfortunate if different matrices were adopted, because then image coding and decoding would depend on whether the picture was small (conventional video) or large (HDTV).
In digital video, Rec. 601 standardizes subsampling denoted 4:2:2, where CB and CR components are subsampled horizontally by a factor of two with respect to luma. JPEG and MPEG conventionally subsample by a factor of two in the vertical dimension as well, denoted 4:2:0.
Colour difference coding is standardized in Rec. 601. For details on colour difference coding as used in video, consult Watkinson [16].
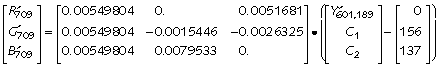
Decoded R'G'B' components from PhotoYCC can exceed unity or go below zero. PhotoYCC extends the Rec. 709 transfer function above unity, and reflects it around zero, to accommodate wide excursions of R'G'B'. To decode to CRT primaries, clip R'G'B' to the range zero to one.
Well OK, just this once. To transform Y', (B'-Y') and (R'-Y') components from Eq 1 to Y'UV, scale (B'-Y') by 0.492111 to get U and scale R'-Y' by 0.877283 to get V. The factors are chosen to limit composite NTSC or PAL amplitude for all legal R'G'B' values:
![]()
To transform to Y' IQ to Y' UV, perform a 33 degree rotation and an exchange of colour difference axes:
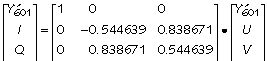
To ensure that your scale factors are correct and that clipping is not being invoked, test 75% bars, a colourbar sequence having 75%-amplitude bars instead of 100%.
The XYZ and RGB systems are far from exhibiting perceptual uniformity. Finding a transformation of XYZ into a reasonably perceptually-uniform space consumed a decade or more at the CIE and in the end no single system could be agreed. So the CIE standardized two systems, L*u*v* and L*a*b*, sometimes written CIELUV and CIELAB. (The u and v are unrelated to video U and V.) Both L*u*v* and L*a*b* improve the 80:1 or so perceptual nonuniformity of XYZ to about 6:1. Both demand too much computation to accommodate real-time display, although both have been successfully applied to image coding for printing.
Computation of CIE L*u*v* involves intermediate u' and v ' quantities, where the prime denotes the successor to the obsolete 1960 CIE u and v system:
![]()
First compute un' and vn' for your reference white Xn , Yn and Zn . Then compute u' and v ` - and L* as discussed earlier - for your colours. Finally, compute:
![]()
L*a*b* is computed as follows, for (X/Xn, Y/Yn, Z/Zn ) > 0.01:
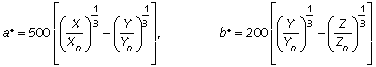
These equations are great for a few spot colours, but no fun for a million pixels. Although it was not specifically optimized for this purpose, the nonlinear R'G'B' coding used in video is quite perceptually uniform, and has the advantage of being fast enough for interactive applications.
Here are some of problems of HSB and HLS. In colour selection where "lightness" runs from zero to 100, a lightness of 50 should appear to be half as bright as a lightness of 100. But the usual formulations of HSB and HLS make no reference to the linearity or nonlinearity of the underlying RGB, and make no reference to the lightness perception of human vision.
The usual formulation of HSB and HLS compute so-called "lightness" or "brightness" as (R+G+B)/3. This computation conflicts badly with the properties of colour vision, as it computes yellow to be about six times more intense than blue with the same "lightness" value (say L=50).
HSB and HSL are not useful for image computation because of the discontinuity of hue at 360 degrees. You cannot perform arithmetic mixtures of colours expressed in polar coordinates.
Nearly all formulations of HSB and HLS involve different computations around 60 degree segments of the hue circle. These calculations introduce visible discontinuities in colour space.
Although the claim is made that HSB and HLS are "device independent", the ubiquitous formulations are based on RGB components whose chromaticities and white point are unspecified. Consequently, HSB and HLS are useless for conveyance of accurate colour information.
If you really need to specify hue and saturation by numerical values, rather than HSB and HSL you should use polar coordinate version of u* and v*: h*uv for hue angle and c*uv for chroma.
A true colour system usually interposes a lookup table between each component of the framestore and each channel to the display. This makes it possible to use a true colour system with either linear or nonlinear coding. In the X Window System, true colour refers to fixed lookup tables, and direct colour refers to lookup tables that are under the control of application software.
The colours in the map may be fixed systematically at the design of a system. As an example, 216 index entries an eight-bit indexed colour system can be partitioned systematically into a 6 x 6 x 6 "cube" to implement what amounts to a direct colour system where each of red, green and blue has a value that is an integer in the range zero to five.
An RGB image can be converted to a predetermined colormap by choosing, for each pixel in the image, the colormap index corresponding to the "closest" RGB triple. With a systematic colormap such as a 6 x 6 x 6 colourcube this is straightforward. For an arbitrary colormap, the colormap has to be searched looking for entries that are "close" to the requested colour. "Closeness" should be determined according to the perceptibility of colour differences. Using colour systems such as CIE L*u*v* or L*a*b* is computationally prohibitive, but in practice it is adequate to use a Euclidean distance metric in R'G'B' components coded nonlinearly according to video practice.
A direct colour image can be converted to indexed colour with an image-dependent colormap by a process of colour quantization that searches through all of the triples used in the image, and chooses the palette for the image based on the colours that are in some sense most "important". Again, the decisions should be made according to the perceptibility of colour differences. Adobe Photoshop[tm] can perform this conversion. UNIX[tm] users can employ the pbm package.
If your system accommodates arbitrary colormaps, when the map associated with the image in a particular window is loaded into the hardware colormap, the maps associated with other windows may be disturbed. In window system such as the X Window System[tm] running on a multitasking operating system such as UNIX, even moving the cursor between two windows with different maps can cause annoying colormap flashing.
An eight-bit indexed colour system requires less data to represent a picture than a twenty-four bit truecolour system. But this data reduction comes at a high price. The truecolour system can represent each of its three components according to the principles of sampled continuous signals. This makes it possible to accomplish, with good quality, operations such as resizing the image. In indexed colour these operations introduce severe artifacts because the underlying representation lacks the properties of a continuous representation, even if converted back to RGB.
In graphic file formats such as GIF of TIFF, an indexed colour image is accompanied by its colormap. Generally such a colormap has RGB entries that are gamma corrected: the colormap's RGB codes are intended to be presented directly to a CRT, without further gamma correction.
If you are using colour to aid in the visual detection of patterns, you should use colours chosen according to the principles of perceptual uniformity. This an open research problem, but basing your system on CIE L*a*b* or L*u*v*, or on nonlinear video-like RGB, would be a good start.
Computer displays are generally viewed from distances where the device pixels subtend a rather large angle at the viewer's eye, relative to his visual acuity. Applying dither to a conventional computer display often introduces objectionable artifacts. However, careful application of dither can be effective. For example, human vision has poor acuity for blue spatial detail but good colour discrimination capability in blue. Blue can be dithered across two-by-two pixel arrays to produce four times the number of blue levels, with no perceptible penalty at normal viewing distances.
Halftone dots are usually placed in a regular grid, although stochastic screening has recently been introduced that modulates the spacing of the dots rather than their size.
In colour printing it is conventional to use cyan, magenta, yellow and black grids that have exactly the same dot pitch but different carefully-chosen screen angles. The recently introduced technique of Flamenco screening uses the same screen angles for all screens, but its registration requirements are more stringent than conventional offset printing.
Agfa's booklet [17] is an excellent introduction to practical concerns of printing. And it's in colour! The standard reference to halftoning algorithms is Ulichney [18], but that work does not detail the nonlinearities found in practical printing systems. For details about screening for colour reproduction, consult Fink [19]. Consult Frequently Asked Questions about Gamma for an introduction to the transfer function of offset printing.
A colour management system (CMS) is a layer of software resident on a computer that negotiates colour reproduction between the application and colour devices. It cooperates with the operating system and the graphics library components of the platform software. Colour management systems perform the colour transformations necessary to exchange accurate colour between diverse devices, in various colour coding systems including RGB, CMYK and CIE L*a*b*.
The CMS makes available to the application a set of facilities whereby the application can determine what colour devices and what colour spaces are available. When the application wishes to access a particular device, it requests that the colour manager perform a mathematical transform from one space to another. The colour spaces involved can be device-independent abstract colour spaces such as CIE XYZ, CIE L*a*b* or calibrated RGB. Alternatively a colour space can be associated with a particular device. In the second case the Colour manager needs access to characterization data for the device, and perhaps also to calibration data that reflects the state of the particular instance of the device.
Sophisticated colour management systems are commercially available from Kodak, Electronics for Imaging (EFI) and Agfa. Apple's ColorSync[tm] provides an interface between a Mac application program and colour management capabilities either built-in to ColorSync or provided by a plug-in. Sun has announced that Kodak's CMS will be shipped with the next version of Solaris.
The basic CMS services provided with desktop operating systems are likely to be adequate for office users, but are unlikely to satisfy high-end users such as in prepress. All of the announced systems have provisions for plug-in colour management modules (CMMs) that can provide sophisticated transform machinery. Advanced colour management modules will be commercially available from third parties.
If you have a device that has not been characterized by its manufacturer, Agfa's FotoTune[tm] software - part of Agfa's FotoFlow[tm] colour manager - can create device profiles.
Use the Rec. 709 primary chromaticities. Your monitor is probably already quite close to this. Rec. 709 has international agreement, offers excellent performance, and is the basis for HDTV development so it's future-proof.
If you need to operate in linear light, so be it. Otherwise, for best perceptual performance and maximum ease of interchange with digital video, use the Rec. 709 transfer function, with its 0.45-power law. If you need Mac compatibility you will have to suffer a penalty in perceptual performance. Raise tristimulus values to the 1/1.8-power before presenting them to QuickDraw.
To code luma, use the Rec. 601 luma coefficients 0.299, 0.587 and 0.114. Use Rec. 601 digital video coding with black at 16 and white at 235.
Use prime symbols ( ' ) to denote all of your nonlinear components!
PhotoCD uses all of the preceding measures. PhotoCD codes colour differences asymmetrically, according to film gamut. Unless you have a requirement for film gamut, you should code into colour differences using Y ` CBCR coding with Rec. 601 studio video (16..235/128+/-112) excursion.
Tag your image data with the primary and white chromaticity, transfer function and luma coefficients that you are using. TIFF 6.0 tags have been defined for these parameters. This will enable intelligent readers, today or in the future, to determine the parameters of your coded image and give you the best possible results.
[2] LeRoy E. DeMarsh and Edward J. Giorgianni, "Color Science for Imaging Systems", Physics Today, September 1989, 44-52.
[3] W.F. Schreiber, Fundamentals of Electronic Imaging Systems, Second Edition (Springer-Verlag, 1991).
[4] Publication CIE No 15.2, Colorimetry, Second Edition (1986), Central Bureau of the Commission Internationale de L'Éclairage, Vienna, Austria.
[5] Günter Wyszecki and W.S. Styles, Color Science: Concepts and Methods, Quantitative Data and Formulae, Second Edition (John Wiley & Sons, New York, 1982).
[6] D.B. Judd and Günter Wyszecki, Color in Business, Science and Industry, Third Edition (John Wiley, New York, 1975).
[7] R.W.G. Hunt, The Reproduction of Colour in Photography, Printing and Television, Fifth Edition (Fountain Press, Tolworth, England, 1995).
[8] ITU-R Recommendation BT.709, Basic Parameter Values for the HDTV Standard for the Studio and for International Programme Exchange (1990), [formerly CCIR Rec. 709], ITU, 1211 Geneva 20, Switzerland.
[9] Bruce J. Lindbloom, "Accurate Color Reproduction for Computer Graphics Applications", Computer Graphics, Vol. 23, No. 3 (July 1989), 117-126 (proceedings of SIGGRAPH '89).
[10] William B. Cowan, "An Inexpensive Scheme for Calibration of a Colour Monitor in terms of CIE Standard Coordinates", Computer Graphics, Vol. 17, No. 3 (July 1983), 315-321.
[11] SMPTE RP 177-1993, Derivation of Basic Television Color Equations.
[12] Television Engineering Handbook, Featuring HDTV Systems, Revised Edition by K. Blair Benson, revised by Jerry C. Whitaker (McGraw-Hill, 1992). This supersedes the Second Edition.
[13] Roy Hall, Illumination and Color in Computer Generated Imagery (Springer-Verlag, 1989).
[14] Chet S. Haase and Gary W. Meyer, "Modelling Pigmented Materials for Realistic Image Synthesis", ACM Transactions on Graphics, Vol. 11, No. 4, 1992, p. 305.
[15] Maureen C. Stone, William B. Cowan and John C. Beatty, "Color Gamut Mapping and the Printing of Digital Color Images", ACM Transactions on Graphics, Vol. 7, No. 3, October 1988.
[16] John Watkinson, An Introduction to Digital Video (Focal Press, Sevenoaks, Kent, England, 1994).
[17] Agfa Corporation, An introduction to Digital Color Prepress, Volumes 1 and 2 (1990), Prepress Education Resources, P.O. Box 7917 Mt.Prospect, IL 60056-7917. 800-395-7007.
[18] Robert Ulichney, Digital Halftoning (MIT Press, Cambridge, MA, 1988).
[19] Peter Fink, PostScript Screening: Adobe Accurate Screens (Adobe Press, 1992).
This note contains some errors: if you find any, please let me know.
I welcome suggestions for additions and improvements.
Poynton - Color page