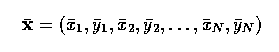55:148 Digital Image Processing
55:247 Image Analysis and Understanding
Chapter 8, Part VI
Image understanding: Semantic image segmentation and understanding
Chapter 8.6 Overview:
Semantic image segmentation and understanding
- This section presents a higher level extension of region growing methods which
were discussed in Chapter 5.
- Algorithms already discussed in Chapter 5 merge regions on the basis of general
heuristics using local properties of regions, and may be referred to as syntactic
information based methods.
- Conversely, semantic information representing higher level knowledge was first used by
Feldman in 1974.
- Including more information, especially information about assumed region interpretation,
can help the merging process.
- Context and criteria for global optimization of region interpretation consistency also
play an important role.
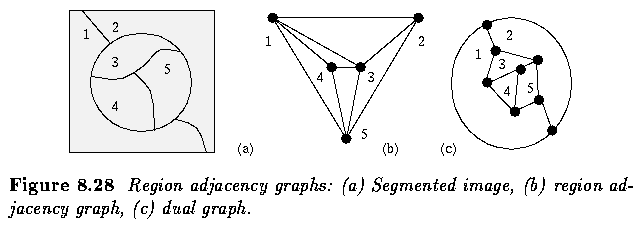
- Representation of image regions and their inter-relationships
- region adjacency graph
- dual graph
- The region adjacency graph is one in which costs are associated with both nodes and
arcs, implying that an update of these costs must be included in the given algorithm as
node costs change due to the connecting two regions R_i and R_j.


Semantic region growing
- Consider remotely sensed photographs, in which regions can be determined with
interpretations such as field, road, forest, town, etc.
- Adjacent regions with the same interpretation can be merged.
- The problem is that the interpretation of regions is not known and the region
description may give unreliable interpretations.
- Then, it is natural to incorporate context into the region merging using a priori
knowledge about relations (unary, binary) among adjacent regions, and then to apply
constraint propagation to achieve globally optimal segmentation and interpretation
throughout the image.
- A region merging segmentation scheme is now considered in which semantic information is
used in later steps, with the early steps being controlled by general heuristics.
- Only after the preliminary heuristics have terminated are semantic properties of
existing regions evaluated, and further region merging is either allowed or restricted.


- The final two steps, where semantic information has been incorporated, represent a
variation of a serial relaxation algorithm combined with a depth-first interpretation tree
search.
- The goal is to maximize an objective function
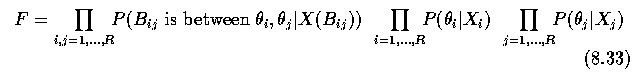
- The probability that a border B_ij between two regions R_i and R_j is a false one
must be found in step (4).
- This probability P can be found as a ratio of conditional probabilities;
- let P_t denote the probability that the boundary should remain,
- let P_f denote the probability that the boundary is false (i.e. should be removed and
the regions should be merged)
- let X(B_{ij}) denote properties of the boundary B_{ij}
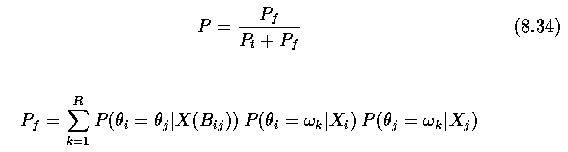
where
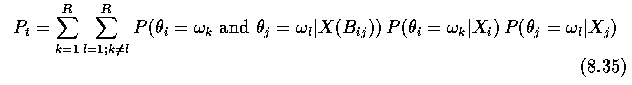
- The confidence C_i of interpretation of the region R_i (step (6)):
- Let theta_i^1, theta_i^2 represent the two most probable interpretations of region R_i.

- After assigning the final interpretation theta_f to a region R_f, interpretation
probabilities of all its neighbors R_j (with non-final labels) are updated to
maximize the objective function
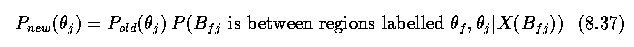
- The computation of these conditional probabilities is very expensive in terms of time
and memory.
- It may be advantageous to precompute them beforehand and refer to table values during
processing; this table must have been constructed with suitable sampling.
- Appropriate models of the inter-relationship between region interpretations, the
collection of conditional probabilities, and methods of confidence evaluation must be
specified to implement this approach.
Genetic image interpretation
- The previous section described the first historical semantic region growing method,
which is still conceptually up to date.
- There is a fundamental problem in the region growing segmentation approach - the
results are sensitive to the split/merge order.
- The conventional split-and-merge approach usually results in an undersegmented or an
oversegmented image.
- It is practically impossible to stop the region growing process with a high confidence
that there are neither too many nor too few regions in the image.
- Region growing can be designed so that it always results in an oversegmented image and
post-processing steps can be used to remove false boundaries.
- False oversegmented regions can be found in watershed segmentation.
- Conventional region growing approaches are based on evaluation of homogeneity
criteria and the goal is either to split a non-homogeneous region or to merge two regions,
which may form a homogeneous region.
- Result is sensitive to the merging order - even if a merge results in a homogeneous
region, it may not be optimal.
- There is no mechanism for seeking the optimal merges.
- The semantic region growing approach to segmentation and interpretation starts with an
oversegmented image in which some merges were not best possible.
- The semantic process is then trying to locate the maximum of some objective function by
grouping regions which may already be incorrect and is therefore trying to obtain an
optimal image interpretation from partially processed data where some significant
information has already been lost.
- Conventional semantic region growing merges regions in an interpretation level only and
does not evaluate properties of newly merged regions.
- It also very often ends in a local optimum of region labeling; the global optimum is not
found because of the character of the optimization.
- Unreliability of image segmentation and interpretation of complex images results.
- The genetic image interpretation method solves these basic problems in the following
manner:
- Both region merging and splitting is allowed; no merge or split is ever final, a better
segmentation is looked for even if the current segmentation is already good.
- Semantics and higher level knowledge are incorporated into the main segmentation
process, not applied as post-processing after the main segmentation steps are over.
- Semantics are included in an objective evaluation function (that is similar to
conventional semantic-based segmentation).
- In contrast to conventional semantic region growing, any merged region is considered a
contiguous region in the semantic objective function evaluation and all its properties are
measured.
- The genetic image interpretation method does not look for local maxima; its search is
likely to yield an image segmentation and interpretation specified by a (near) global
maximum of an objective function
- The genetic image interpretation method is based on a hypothesize and verify
principle.
- An objective function which evaluates the quality of a segmentation and interpretation
is optimized by a genetic algorithm.
- The method is initialized with an oversegmented image called a primary segmentation,
in which starting regions are called primary regions.
- Primary regions are repeatedly merged into current regions during the segmentation
process.
- The genetic algorithm is responsible for generating new populations of feasible
image segmentation and interpretation hypotheses.
- Genetic algorithms test the whole population of segmentations, the better segmentations
survive, and others die.
- If the objective function suggests that some merge of image regions was a good merge, it
is allowed to survive into the next generation of image segmentation (the code string
describing that particular segmentation survives), while bad region merges are removed
(their description code strings die).
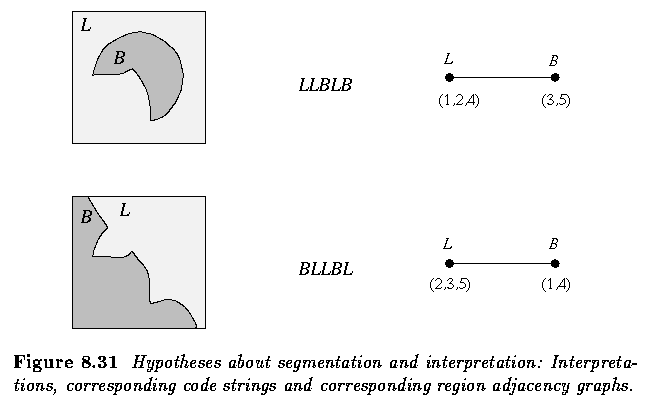
- The primary region adjacency graph is the adjacency graph describing the primary
image segmentation.
- The specific region adjacency graph represents an image after the merging of all
adjacent regions of the same interpretation into a single region (collapsing the primary
region adjacency graph).
- The genetic algorithm requires any member of the processed population to be represented
by a code string.
- Each feasible image segmentation defined by a generated code string (segmentation
hypothesis) corresponds to a unique specific region adjacency graph.
- The specific region adjacency graphs serve as tools for evaluating objective
segmentation functions.
- Design of a segmentation optimization function (the fitness function in genetic
algorithms), is crucial for a successful image segmentation.
- The conventional approach evaluates image segmentation and interpretation confidences of
all possible region interpretations.
- Based on the region interpretations and their confidences, the confidences of
neighboring interpretations are updated, some being supported, and others becoming less
probable.
- This conventional method can easily end at a consistent but sub-optimal image
segmentation and interpretation.
- In the genetic approach, the algorithm is fully responsible for generating new and
increasingly better hypotheses about image segmentation.
- Only these hypothetical segmentations are evaluated by the objective function.
- Another significant difference is in the region property computation - as mentioned
earlier, a region consisting of several primary regions is treated as a single region in
the property computation process which gives a more appropriate region description.
- Optimization criteria consist of three parts.
- A confidence in the interpretation theta_i of the region R_i according to the region
properties X_i
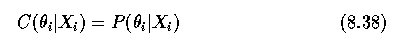
- A confidence in the interpretation theta_i of a region R_i according to the
interpretations theta_j of its neighbors R_j
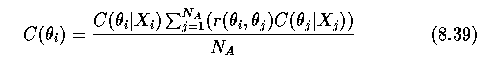
- where r(theta_i,theta_j) represents the value of a compatibility function of two
adjacent objects R_i and R_j with labels \theta_i and \theta_j
- N_A is the number of regions adjacent to the region R_i,
- An evaluation of interpretation confidences in the whole image
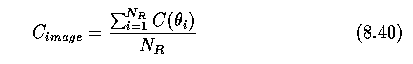
or
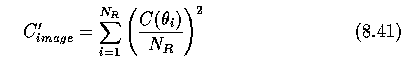
- where N_R is the number of regions in the corresponding specific region adjacency graph.
\
- The genetic algorithm attempts to optimize the objective function C_{image}, which
represents the confidence in the current segmentation and interpretation hypothesis.
- As presented, the segmentation optimization function is based on both unary properties
of hypothesized regions and on binary relations between these regions and their
interpretations.
- The method is described by the following algorithm:


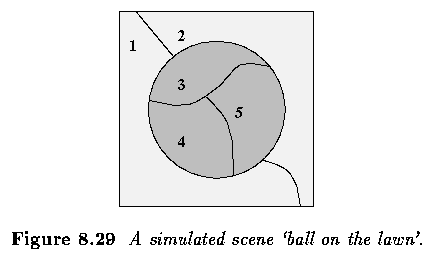
A simple example - Ball on the lawn
- B - ball
- L - lawn
- Knowledge:
- There is a circular ball in the image
- The ball is inside the green lawn region
- In reality, some more a priori knowledge would be added even in this simple example but
this knowledge will be sufficient for our purposes.
- The knowledge must be stored in appropriate data structures.
- Unary condition:
- Let the confidence that a region is a ball be based on its compactness.

- Let the confidence that a region is lawn be based on its greenness.
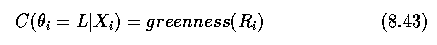
- Let the confidences for regions forming a perfect ball and perfect lawn be equal to one
- Let the confidence that one region is positioned inside the other be given by a
compatibility function
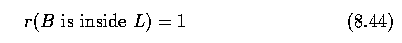
- Let the confidences of all other positional combinations be equal to zero.
- The unary condition says that the more compact a region is, the better its circularity,
and the higher the confidence that its interpretation is a ball.
- The binary condition is very strict and claims that a ball can only be completely
surrounded by a lawn.
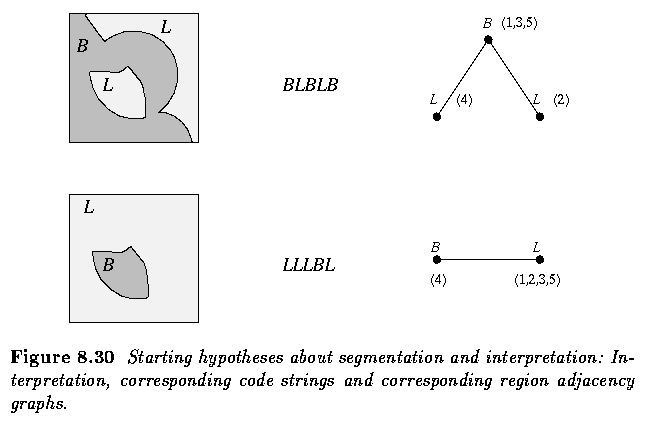
- Primary image segmentation:
- For simplicity, let the starting population of segmentation hypotheses consist of just
two strings.
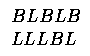
- After a random crossover:
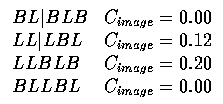
- The second and the third segmentation hypotheses are the best ones, so they are
reproduced and another crossover is applied; the first and the fourth code strings die:
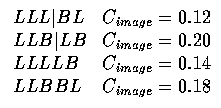
- After one more crossover:
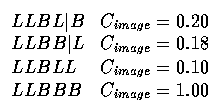
- The code string (segmentation hypothesis) LLBBB has a high (the highest achievable)
confidence.

Brain segmentation example
- The previous example only illustrated the basic principles of the method.
- Practical applications require more complex a priori knowledge, the genetic algorithm
has to work with larger string populations, the primary image segmentation has more
regions, and the optimum solution is not found in three steps.
- Nevertheless the principles remain the same as was demonstrated when the method is
applied to more complex problems
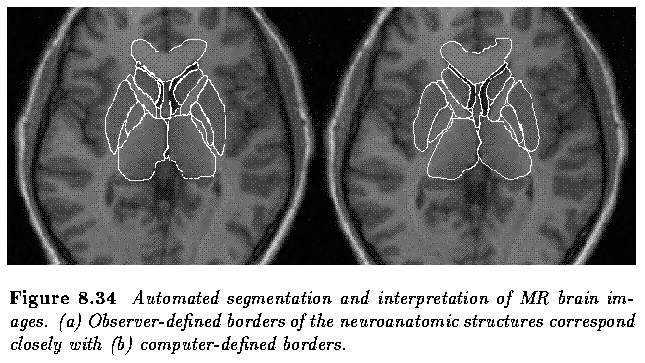
- Interpretation of human magnetic resonance brain images is given here as such a complex
example.
- The genetic image interpretation method was trained on two-dimensional MR images
depicting anatomically-corresponding slices of the human brain.
- Knowledge about the unary properties of the specified neuroanatomic structures and about
the binary properties between the structure pairs was acquired from manually traced
contours in a training set of brain images.
- The unary region confidences C(theta_i | X_i) and the compatibility functions
r(theta_i,theta_j) were calculated based on the brain anatomy and MR image acquisition
parameters.
- Unary Confidences:
- The unary confidence of a region was calculated by matching the region's shape and other
characteristic properties with corresponding properties representing the hypothesized
interpretation.
- Let the set of properties of region R_i be X_i = {x_i1,x_i2,...,x_iN}.
- Matching was done for each characteristic of the region {x_ij}, and the unary confidence
C(theta_i | X_i) was calculated as follows:
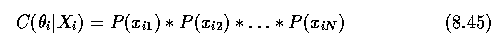
- The feature confidences P(x_ik) were calculated by using the piecewise linear function
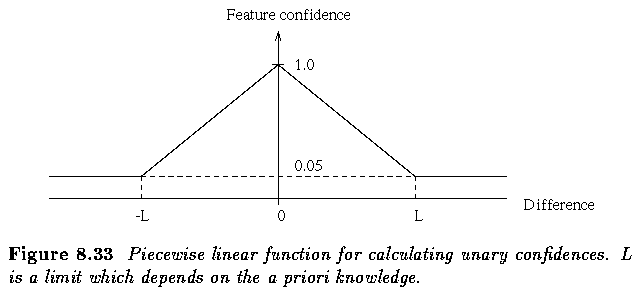
- For example, let x_ik be the area of region R_i in the specific RAG and let R_i be
labeled theta_i.
- According to a priori knowledge, assume that an object labeled theta_i has an area y_ik.
- Then
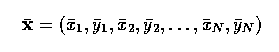
- The limit L depends on the strength of the a priori knowledge for each particular
feature.
- The value of the compatibility function r(theta_i,theta_j) was assigned to be in the
range [0,1] depending on the strength of the a priori knowledge about the expected
configuration of regions R_i and R_j.
- Low binary confidences serve to penalize infeasible configurations of pairs of regions.
- Similarly to the calculation of the unary confidence, the compatibility function was
calculated as a product of local binary relations.
- After the objective function C_image was designed using a number of brain images from
the training set, the genetic brain image interpretation method was applied to testing
brain images.
- For illustration, the primary region adjacency graph typically consisted of
approximately 400 regions; a population of 20 strings and a mutation rate mu =
1/string_length were used during the genetic optimization.
- The method was applied to a testing set of MR brain images and offered good image
interpretation performance.
- Conventional semantic region growing methods start with a non-semantic phase and use
semantic post processing to assign labels to regions.
- Based on the segmentation achieved in the region growing phases, the labeling
process is trying to find a consistent set of interpretations for regions.
- The genetic image interpretation approach functions in a quite different way.
- Firstly, there are not separate phases.
- The semantics are incorporated into the segmentation/interpretation process.
- Secondly, segmentation hypotheses are generated first, and the optimization function is
used only for evaluation of hypotheses.
- Thirdly, a genetic algorithm is responsible for generating segmentation hypotheses in an
efficient way.
- The method can be based on any properties of region description and on any relations
between regions.
- The basic idea of generating segmentation hypotheses solves one of the problems of
split-and-merge region growing - the sensitivity to the order of region growing.
- The only way to re-segment an image in a conventional region growing approach if the
semantic post-processing does not provide a successful segmentation is to apply feedback
control to change region growing parameters in a particular image part.
- There is no guarantee that a global segmentation optimum will be obtained even after
several feedback re-segmentation steps.
- In the genetic image interpretation approach, no region merging is ever final.
- Natural and constant feedback is contained in the genetic interpretation method because
it is a part of the general genetic algorithm - this gives a good chance that a
(near) global optimum segmentation/interpretation will be found in a single processing
stage.
- Note that the image interpretation / understanding methods cannot and do not guarantee a
correct segmentation - all the approaches try to achieve optimality according to the
chosen optimization function.
- Therefore, a priori knowledge is essential to design a good optimization function.
- A priori knowledge is often included into the optimization function in the form of
heuristics.
- In the GA method, it may affect the choice of the starting population of segmentation
hypotheses that can affect computational efficiency.
- Another important property of the GA method is the possibility of parallel
implementation.
- This method is naturally parallel.
- Moreover, there is a straightforward generalization leading to a genetic image
segmentation and interpretation in three dimensions.
- Considering a set of image planes forming a three-dimensional image (like MR or CT
images), a primary segmentation can consist of regions in all image planes and can be
represented by a 3D primary relational graph.
- The interesting possibility is to look for a global three-dimensional segmentation and
interpretation optimum using 3D properties of generated 3D regions in a single
complex processing stage.
- In such an application, the parallel implementation would be a necessity.
Last Modified: February 18, 1997
![[Go Back]](../IMAGES/next.gif)






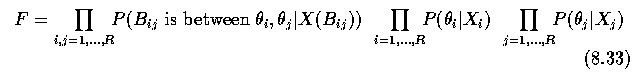
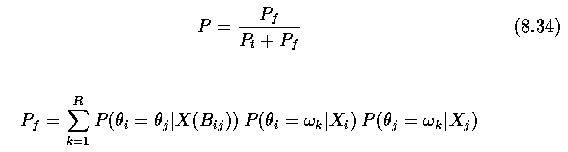
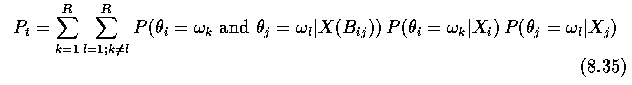

![]()
![]()
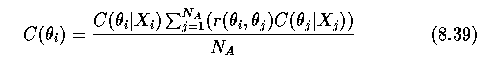
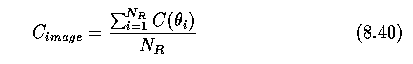
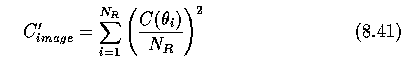




![]()
![]()

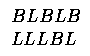
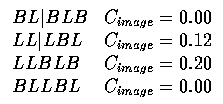
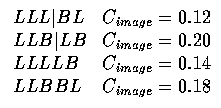
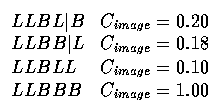


![]()