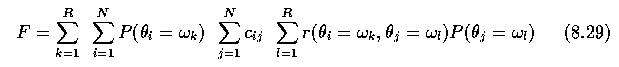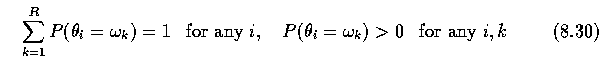55:148 Digital Image Processing
55:247 Image Analysis and Understanding
Chapter 8, Part V
Image understanding: Scene labeling and constraint propagation
Chapter 8.5 Overview:
Scene labeling and constraint propagation
- Context plays a significant role in image understanding; the previous section was
devoted to context present in pixel data configurations, and this section deals with
semantic labeling of regions and objects.
- Assume that regions have been detected in an image that correspond to objects or other
image entities, and let the objects and their inter-relationships be described by a region
adjacency graph and/or a semantic net.
- Object properties are described by unary relations, and inter-relationships between
objects are described by binary (or n-ary) relations.
- The goal of scene labeling is to assign a label (a meaning) to each image object to
achieve an appropriate image interpretation.
- The resulting interpretation should correspond with available scene knowledge.
- The labeling should be consistent, and should favor more probable interpretations if
there is more than one option.
- Consistency means that no two objects of the image appear in an illegal
configuration - e.g. an object labeled house in the middle of an object labeled lake
will be considered inconsistent in most scenes.
- Conversely, an object labeled house surrounded by an object labeled lawn
in the middle of a lake may be fully acceptable.
- Two main approaches may be chosen to achieve this goal.
- Discrete labeling allows only one label to be assigned to each object in the
final labeling.
- Effort is directed to achieving a consistent labeling all over the image.
- Probabilistic labeling allows multiple labels to co-exist in objects.
- Labels are probabilistically weighted, with a label confidence being assigned to each
object label.
- The main difference is in interpretation robustness.
- Discrete labeling always finds either a consistent labeling or detects the impossibility
of assigning consistent labels to the scene.
- Often, as a result of imperfect segmentation, discrete labeling fails to find a
consistent interpretation even if only a small number of local inconsistencies is
detected.
- Probabilistic labeling always gives an interpretation result together with a measure of
confidence in the interpretation.
- Even if the result may be locally inconsistent, it often gives a better scene
interpretation than a consistent and possibly very unlikely interpretation resulting from
a discrete labeling.
- Note that discrete labeling may be considered a special case of probabilistic labeling
with one label probability always being 1 and all the others being 0 for each
object.
- The scene labeling problem is specified by
- A set of objects R_i, i=1,...,N.
- A finite set of labels Omega_i for each object R_i.
- A finite set of relations between objects
- The existence of a compatibility function (reflecting constraints) between interacting
objects.
- To solve the labeling problem considering direct interaction of all objects in an image
is computationally very expensive and approaches to solving labeling problems are usually
based on constraint propagation.
- This means that local constraints result in local consistencies (local optima), and by
applying an iterative scheme the local consistencies adjust to global consistencies
(global optima) in the whole image.
- Many types of relaxation exist, some of them being used in statistical physics, for
example, simulated annealing, stochastic relaxation, etc.
- Others, such as relaxation labeling, are typical in image understanding.
- To provide a better understanding of the idea, the discrete relaxation approach is
considered first.
Discrete relaxation
- Next, six objects are present in the scene, including the background.
- Let the labels be background (B), window (W), table (T), drawer (D), phone (P),
and let the unary properties of object interpretations be
- A window is rectangular
- A table is rectangular
- A drawer is rectangular
- Let the binary constraints be
- A window is located above a table
- A phone is above a table
- A drawer is inside a table
- Background is adjacent to the image border
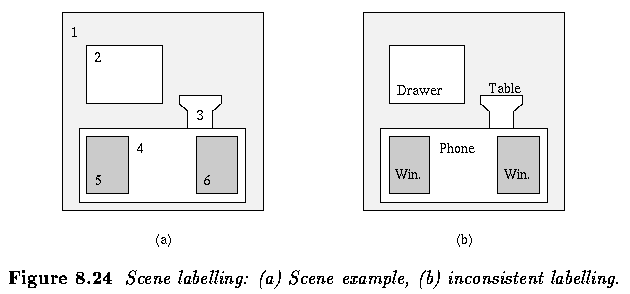
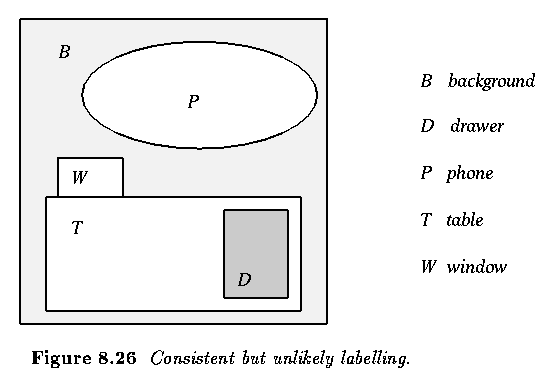
- Given these constraints, the labeling in the right panel is inconsistent.
- Discrete relaxation assigns all existing labels to each object and iteratively removes
all the labels which may not be assigned to an object without violating the constraints.

- A possible relaxation sequence is shown.
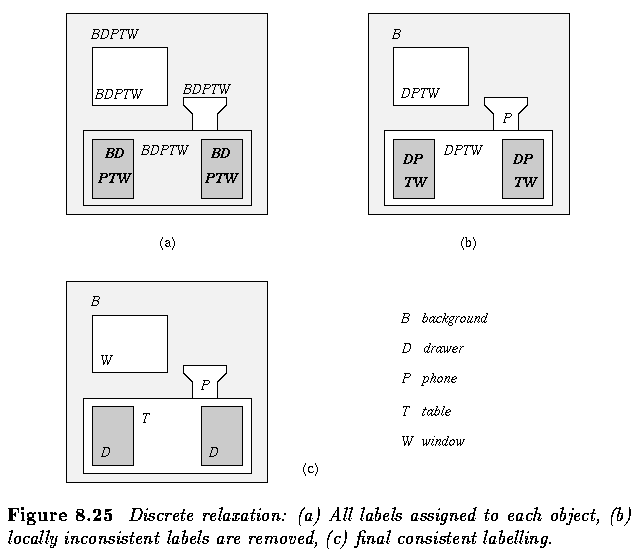
- Note the mechanism of constraint propagation.
- The distant relations between objects may influence labeling in distant locations of the
scene after several steps, making it possible to achieve a global labeling consistency of
the scene interpretation although all the label removing operations are local.
Probabilistic relaxation
- Constraints are a typical tool in image understanding.
- The classical problem of discrete relaxation labeling was first introduced by Waltz in
1957 in understanding perspective line drawings, depicting 3D objects.
- Discrete relaxation results in an unambiguous labeling, however in a majority of real
situations, it represents an oversimplified approach to image data understanding; it
cannot cope with incomplete or imprecise segmentation.
- Using semantics and knowledge, image understanding is supposed to solve segmentation
problems which cannot be solved by bottom-up interpretation approaches.
- Probabilistic relaxation may overcome the segmentation problems of missing objects or
extra regions in the scene, however it results in an ambiguous image interpretation which
is often inconsistent.
- Consider the relaxation problem as specified above (regions R_i and sets of labels
Omega_i) and in addition, let each object R_i be described by a set of unary properties
X_i.
- Similarly to discrete relaxation, object labeling depends on the object properties and
on a measure of compatibility of the potential object labels with the labeling of other
directly interacting objects.
- All the image objects may be considered directly interacting and a general form of the
algorithm will be given assuming this.
- Nevertheless, only adjacent objects are usually considered to interact directly to
reduce computational demands of the relaxation.
- However, as before, more distant objects still interact with each other as a result of
the constraint propagation.
- A region adjacency graph is usually used to store the adjacency information.
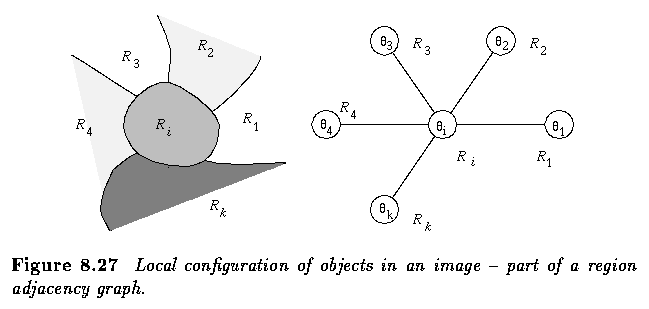
- Confidence in the label theta_i of an object R_i depends on the configuration of
labels of directly interacting objects.
- Let r(theta_i=omega_k, theta_j=omega_l) represent the value of a compatibility function
for two interacting objects R_i and R_j with labels theta_i and theta_j (the probability
that two objects with labels theta_i and theta_j appear in a specific relation).
- The relaxation algorithm is iterative and its goal is to achieve the locally best
consistency in the entire image.
- The support q_j^s for a label theta_i of the object R_i resulting from the binary
relation with the object R_j at the s-th step of the iteration process is
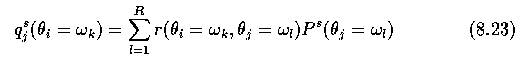
- where P^s(theta_j=omega_l) is the probability that region R_j should be labeled omega_l.
- The support Q^s for the same label theta_i of the same object R_i resulting from
all N directly interacting objects R_j and their labels theta_j at the s-th step is
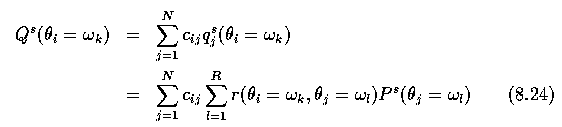
- where c_ij are positive weights with a unit sum.
- The coefficients c_ij represent the strength of interaction between objects R_i and R_j.
- Originally, an updating formula was given which specified the new probability of a label
theta_i according to the previous probability P^s(theta_i=omega_k) and probabilities
of labels of interacting objects
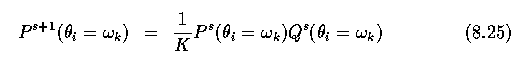
- where K is a normalizing constant
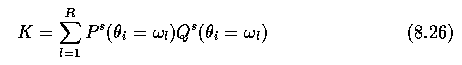
- This form of the algorithm is usually referred to as a nonlinear relaxation scheme.
- A linear scheme looks for probabilities such as
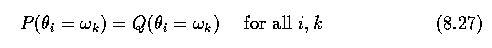
- with a non-contextual probability
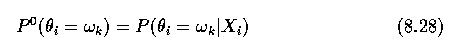
being used only to start the relaxation process
- A relaxation algorithm can also be treated as an optimization problem, the goal being
maximization of the global confidence in the labeling.
- The global objective function is
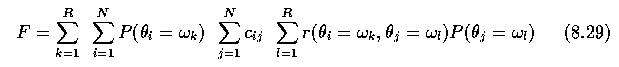
- subject to the constraint that the solution satisfies
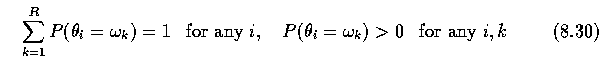
- Optimization approaches to relaxation can be generalized to allow n-ary relations among
objects.
- Convergence is an important property of iterative algorithms; as far as relaxation is
concerned, convergence problems have not yet been satisfactorily solved.
- Although convergence of a discrete relaxation scheme can always be achieved by an
appropriate design of label updating scheme (e.g. to remove the inconsistent labels),
convergence of more complex schemes where labels may be added, or of probabilistic
relaxation, often cannot be guaranteed mathematically.
- Despite this fact, the relaxation approach may still be quite useful.
- Relaxation algorithms are one of the cornerstones of the high-level vision understanding
processes, and applications can also be found outside the area of computer vision.
- Relaxation algorithms are naturally parallel since the label updating may be done
on all objects at the same time.
- Many parallel implementations exist and parallel relaxation does not differ in essence
from the serial version. A general version is


- Relaxation algorithms are still being developed.
- One existing problem with their behavior is that the labeling improves rapidly during
early iterations followed by a degradation, which may be very severe.
- The reason is that the search for the global optimum over the image may cause highly
non-optimal local labeling.
- A possible treatment that allows spatial consistency to be developed while avoiding
labeling degradation is based on decreasing the neighborhood influence with the iteration
count.
Searching interpretation trees
- Note that relaxation is not the only way to solve discrete labeling problems and
classical methods of interpretation tree searching may be applied.
- A tree has as many levels as there are objects present in the scene; nodes are assigned
all possible labels, and a depth-first search based on backtracking is applied.
- Starting with a label assigned to the first object node (tree root), a consistent label
is assigned to the second object node, to the third object node, etc.
- If a consistent label cannot be assigned, a backtracking mechanism changes the label of
the closest node at the higher level.
- All the label changes are done in a systematic way.
- An interpretation tree search tests all possible labelings, and therefore computational
inefficiency is common, especially if an appropriate tree pruning algorithm is not
available.
- An efficient method for searching the interpretation trees was introduced by Grimson.
- The search is heuristically guided towards a good interpretation based on a quality
of match that is based on constraints and may thus reflect feasibility of the
interpretation.
- Clearly, an infeasible interpretation makes all interpretations represented down the
tree infeasible also.
- To represent the possibility of discarding the evaluated patch, an additional
interpretation tree branch is added to each node.
- The general search strategy is based on a depth-first approach in which the search is for
the best interpretation.
- However, the search for the best solution can be very time consuming.
Last Modified: April 1, 1997
![[Go Back]](../IMAGES/next.gif)






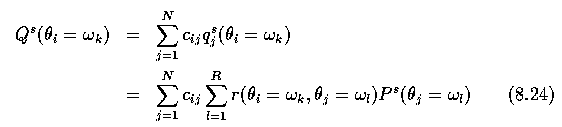
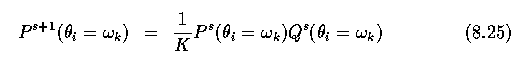
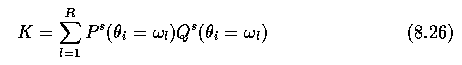
![]()