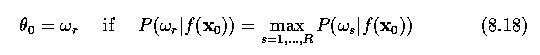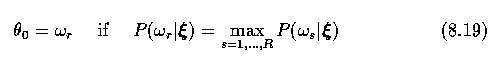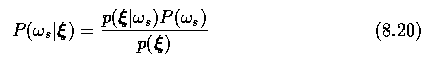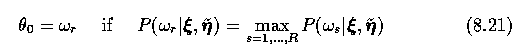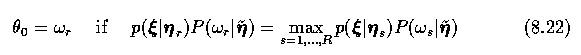55:148 Digital Image Processing
55:247 Image Analysis and Understanding
Chapter 8, Part IV
Image understanding: Pattern recognition methods in image understanding
Chapter 8.4 Overview:
Pattern recognition methods in image understanding
- Pattern recognition methods frequently appear in image understanding.
- Classification-based segmentation of multispectral images (satellite images, magnetic
resonance medical images, etc.) is a typical example.
- Supervised methods are used for classification, a priori knowledge is applied to
form a training set.
- In the image understanding stage, feature vectors derived from local multispectral image
values of image pixels are presented to the classifier which assigns a label to each pixel
of the image.
- Image understanding is then achieved by pixel labeling.
- Thus the understanding process segments a multispectral image into regions of known
labels.
- Training set construction, and therefore human interaction, is necessary for supervised
classification methods, but if unsupervised classification is used, training set
construction is avoided.
- As a result, the clusters and the pixel labels do not have a one-to-one correspondence
with the class meaning.
- This implies the image is segmented, but labels are not available to support image
understanding.
- Fortunately, a priori information can often be used to assign appropriate labels to the
clusters without direct human interaction.
Contextual image classification
- The method presented above works well in non-noisy data, and if the spectral properties
determine classes sufficiently well.
- If noise or substantial variations in in-class pixel properties are present, the
resulting image segmentation may have many small (often one-pixel) regions, which are
misclassified.
- Several standard approaches can be applied to avoid this misclassification, which is
very common in classification-based labeling.
- All of them use contextual information to some extent
- Post-processing filter to a labeled image
- Small or single-pixel regions then disappear as the most probable label from the local
neighborhood is assigned to them.
- This approach works well if the small regions are caused by noise.
- Unfortunately, the small regions can result from true regions with different properties
in the original multispectral image, and in this case such filtering would worsen labeling
results.
- Post-processing filters are widely used in remote sensing applications
- Post-processing classification improvement
- Pixel labels resulting from pixel classification in a given neighborhood form a new
feature vector for each pixel, and a second-stage classifier based on the new feature
vectors assigns final pixel labels.
- The contextual information is incorporated in the labeling process of the second-stage
classifier learning.
- Context may also be introduced in earlier stages, merging pixels into homogeneous
regions and classifying these regions.
- Another contextual pre-processing approach is based on acquiring pixel feature
descriptions from a pixel neighborhood.
- Mean values, variances, texture description, etc. may be added to (or may replace)
original spectral data.
- This approach is very common in textured image recognition.
- The most interesting option is to combine spectral and spatial information in the same
stage of the classification process.
- The label assigned to each image pixel depends not only on multispectral gray level
properties of the particular pixel but also considers the context in the pixel
neighborhood.
- The last approach is discussed in more detail.
- Contextual classification of image data is based on the Bayes minimum error classifier.
- For each pixel x0, a vector consisting of (possibly multispectral) values f(xi)
of pixels in a specified neighborhood N(x0) is used as a feature representation
of the pixel x0. Each pixel is represented by the vector
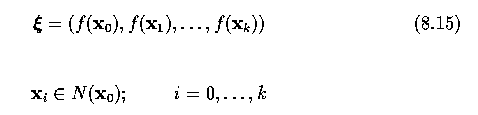
- Some more vectors are defined which will be used later.
- Let labels (classification) of pixels in the neighborhood N(x0) be
represented by a vector
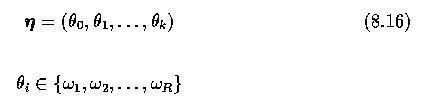
- and omegas denotes the assigned class.
- Further, let the labels in the neighborhood excluding the pixel x0 be
represented by a vector

- Theoretically, there may be no limitation on the neighborhood size, but the majority of
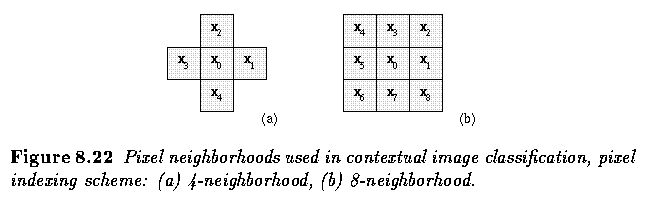
contextual information is believed to be present in a small neighborhood of the pixel x0.
- Therefore, a 3 x 3 neighborhood in 4-connectivity or in 8-connectivity is usually
considered appropriate.
- Also, computational demands increase exponentially with growth of neighborhood size.
- A conventional minimum error classification method assigns a pixel x0 to a
class omegar if the probability of x0 being from the class omegar
is the highest of all possible classification probabilities
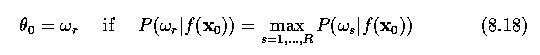
- A contextual classification scheme uses the feature vector xi instead of x0,
and the decision rule remains similar
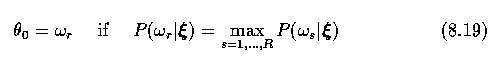
- The a posteriori probability P(omegas|xi) can be computed using the Bayes
formula
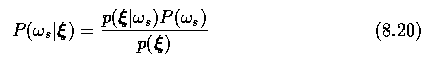
- Note that each image pixel is classified using a corresponding vector xi from its
neighborhood, and so there are as many vectors xi as there are pixels in the image.
- The basic contextual classification algorithm can be summarized as

- A substantial limitation in considering larger contextual neighborhoods is exponential
growth of computational demands with increasing neighborhood size.
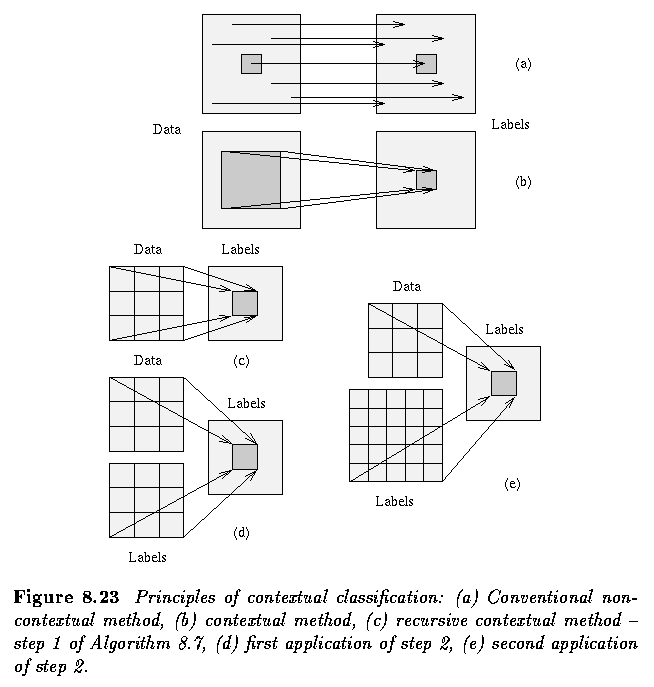
- A recursive contextual classification overcomes these difficulties.
- The main trick of this method is in propagating contextual information through the image
although the computation is still kept in small neighborhoods.
- Spectral and neighborhood pixel labeling information are both used in classification.
- Context from a distant neighborhood can propagate to the labeling theta0 of
the pixel x0
- The vector ~eta of labels in the neighborhood may further improve the contextual
representation.
- Clearly, if the information contained in the spectral data in the neighborhood is
unreliable (e.g. based on spectral data, the pixel x0 may be classified into a
number of classes with similar probabilities) the information about labels in the
neighborhood may increase confidence in one of those classes.
- If a majority of surrounding pixels are labeled as members of a class omegai,
the confidence that the pixel x0 should also be labeled omegai
increases.
- More complex dependencies may be found in the training set - for instance imagine a thin
striped noisy image. Considering labels in the neighborhood of the pixel x0,
the decision rule becomes
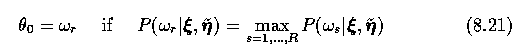
- After several applications of the Bayes formula the decision rule transforms into
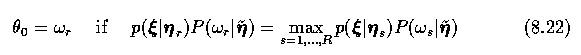
where etar is a vector eta with theta0=omegar.
- Assuming all necessary probability distribution parameters were determined in the
learning process, the recursive contextual classification algorithm follows:

- There is a crucial idea incorporated in the algorithm of recursive contextual image
classification that will be seen several times throughout this chapter; this is the idea
of information propagation from distant image locations without the necessity for
expensive consideration of context in large neighborhoods.
- This is a standard approach used in image understanding.
Last Modified: April 1, 1997
![[Go Back]](../IMAGES/next.gif)
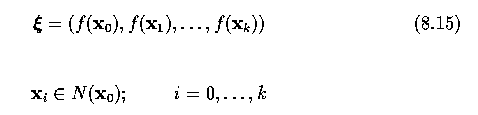
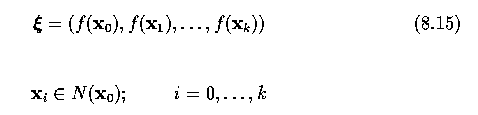
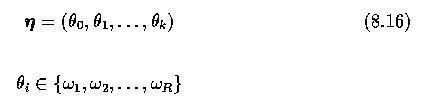
![]()