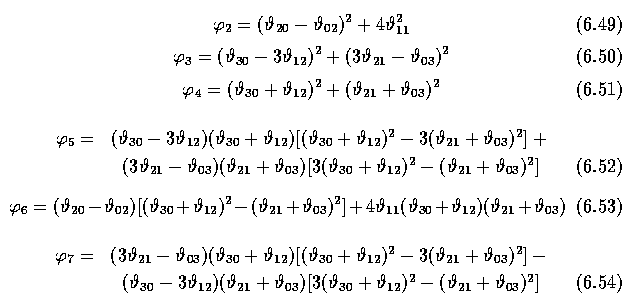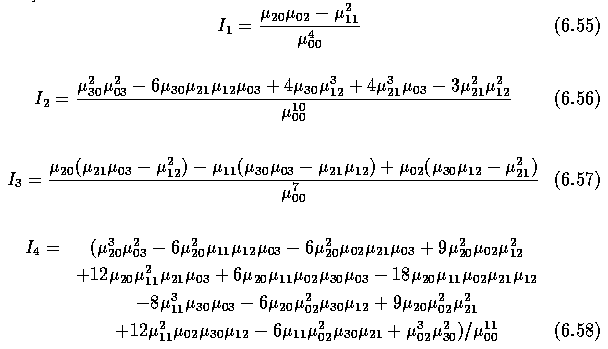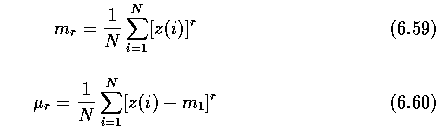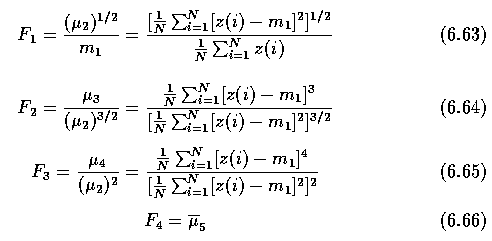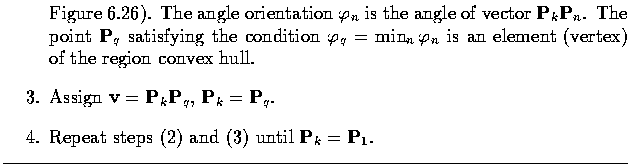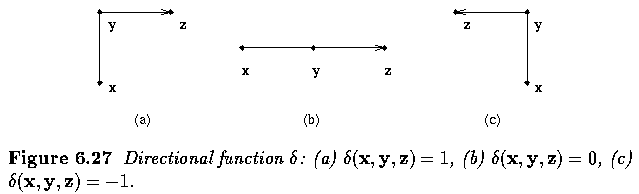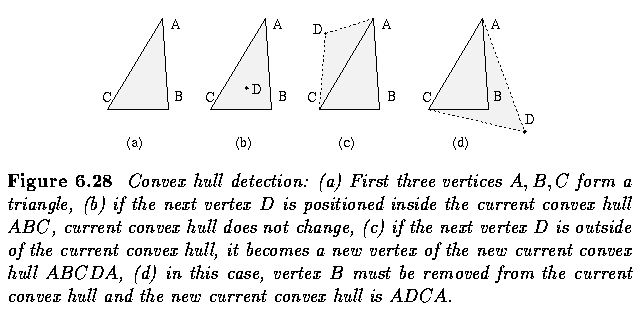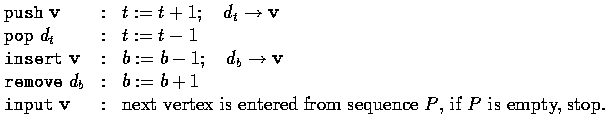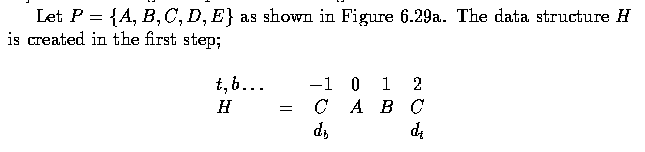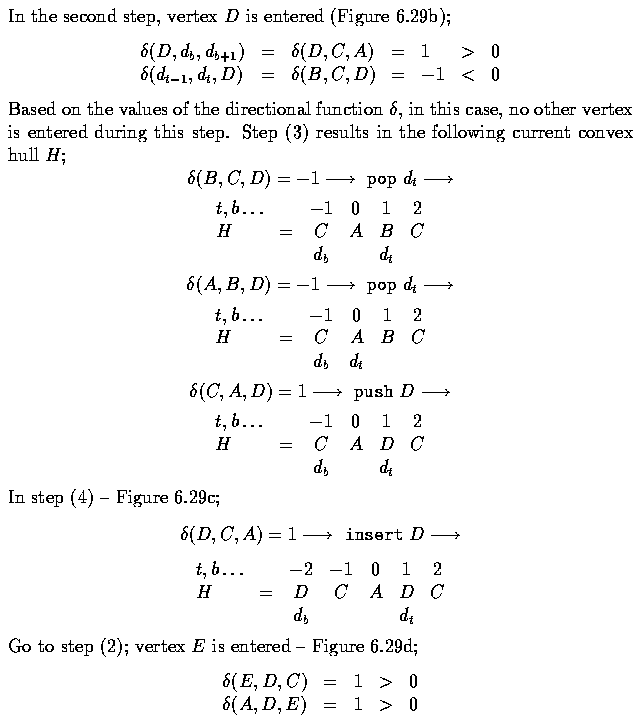55:148 Digital Image Processing
55:247 Image Analysis and Understanding
Chapter 6, Part III
Shape representation and description: Region-based shape representation and description
Chapter 6.3 Overview:
Region-based shape representation and
description
Simple scalar region descriptors
- A large group of shape description techniques is represented by heuristic approaches
which yield acceptable results in description of simple shapes.
- Heuristic region descriptors:
- area,
- rectangularity,
- elongatedness,
- direction,
- compactness,
- etc.
- These descriptors cannot be used for region reconstruction and do not work for more
complex shapes.
- Procedures based on region decomposition into smaller and simpler subregions must be
applied to describe more complicated regions, then subregions can be described separately
using heuristic approaches.
- Simple scalar region descriptors
- Area is given by the number of pixels of which the region consists.
- The real area of each pixel may be taken into consideration to get the real
size of a region.
- If an image is represented as a rectangular raster, simple counting of region pixels
will provide its area.
- If the image is represented by a quadtree, then:

- The region can also be represented by n polygon vertices
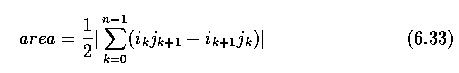
the sign of the sum represents the polygon orientation.
- If the region is represented by the (anti-clockwise) Freeman chain code the following
algorithm provides the area


- Euler's number
- (sometimes called Genus or the Euler-Poincare characteristic) describes a
simple topologically invariant property of the object.
- S is the number of contiguous parts of an object and N is the number of holes in the
object (an object can consist of more than one region).

- Projections
- Horizontal and vertical region projections
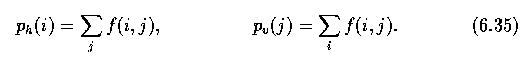
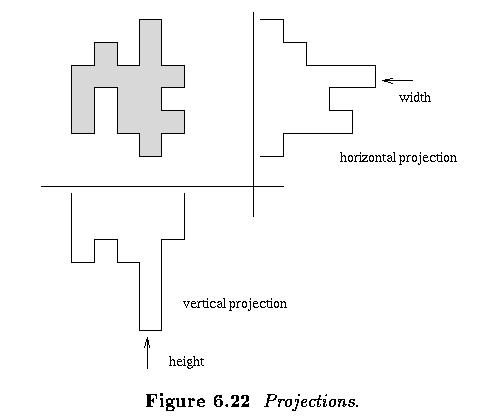
- Eccentricity
- The simplest is the ratio of major and minor axes of an object.
- Elongatedness
- A ratio between the length and width of the region bounding rectangle.
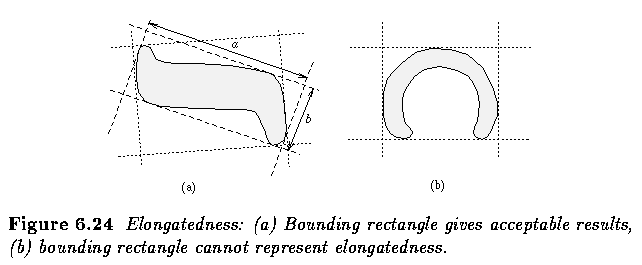
- This criterion cannot succeed in curved regions, for which the evaluation of
elongatedness must be based on maximum region thickness.
- Elongatedness can be evaluated as a ratio of the region area and the square of its
thickness.
- The maximum region thickness (holes must be filled if present) can be determined as the
number d of erosion steps that may be applied before the region totally disappears.
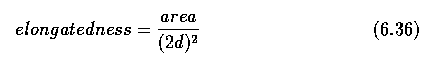
- Rectangularity
- Let F_k be the ratio of region area and the area of a bounding rectangle, the rectangle
having the direction k. The rectangle direction is turned in discrete steps as before, and
rectangularity measured as a maximum of this ratio F_k
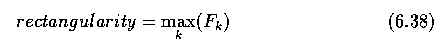
- Direction
- Direction is a property which makes sense in elongated regions only.
- If the region is elongated, direction is the direction of the longer side of a minimum
bounding rectangle.
- If the shape moments are known, the direction \theta can be computed as
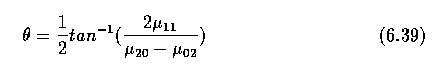
- Elongatedness and rectangularity are independent of linear transformations --
translation, rotation, and scaling.
- Direction is independent on all linear transformations which do not include rotation.
- Mutual direction of two rotating objects is rotation invariant.
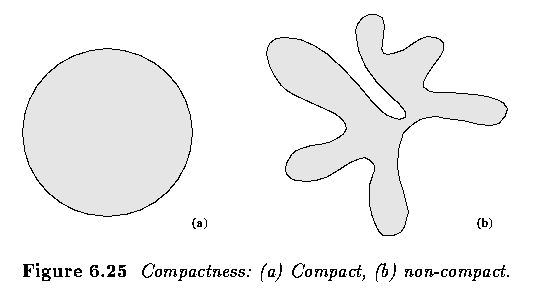
- Compactness
- Compactness is independent of linear transformations

- The most compact region in a Euclidean space is a circle.
- Compactness assumes values in the interval [1,infty) in digital images if the boundary
is defined as an inner boundary, while using the outer boundary, compactness assumes
values in the interval [16,infty).
- Independence from linear transformations is gained only if an outer boundary
representation is used.
Moments
- Region moment representations interpret a normalized gray level image function as a
probability density of a 2D random variable.
- Properties of this random variable can be described using statistical characteristics - moments.
- Assuming that non-zero pixel values represent regions, moments can be used for binary or
gray level region description.
- A moment of order (p+q) is dependent on scaling, translation, rotation, and even on gray
level transformations and is given by
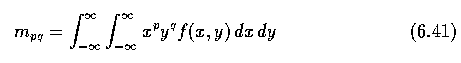
- In digitized images we evaluate sums
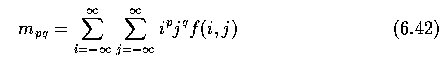
- where x,y,i,j are the region point co-ordinates (pixel co-ordinates in digitized
images).
- Translation invariance can be achieved if we use the central moments
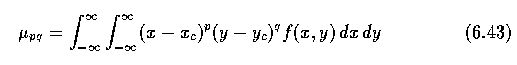
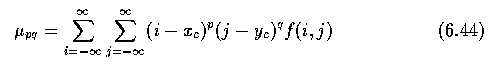
- where x_c, y_c are the co-ordinates of the region's centroid

- In the binary case, m_00 represents the region area.
- Scale invariant features can also be found in scaled central moments
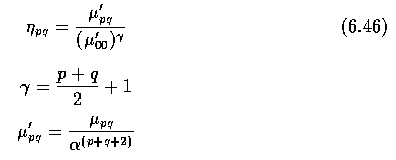
and normalized unscaled central moments

- Rotation invariance can be achieved if the co-ordinate system is chosen such that mu_11
= 0.
- A less general form of invariance is given by seven rotation, translation, and scale
invariant moment characteristics

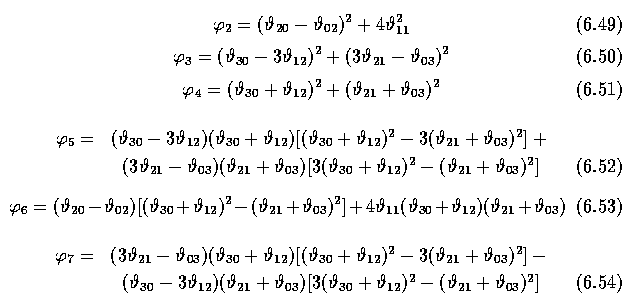
- While the seven moment characteristics presented above were shown to be useful, they are
only invariant to translation, rotation, and scaling.
- A complete set of four affine moment invariants derived from second- and third-order
moments is
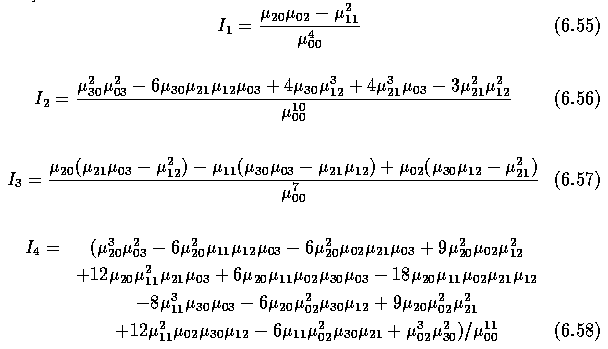
- All moment characteristics are dependent on the linear gray level transformations of
regions; to describe region shape properties, we work with binary image data (f(i,j)=1 in
region pixels) and dependence on the linear gray level transform disappears.
- Moment characteristics can be used in shape description even if the region is
represented by its boundary.
- A closed boundary is characterized by an ordered sequence z(i) that represents the
Euclidean distance between the centroid and all N boundary pixels of the digitized shape.
- No extra processing is required for shapes having spiral or concave contours.
- Translation, rotation, and scale invariant one-dimensional normalized contour sequence
moments can be estimated as
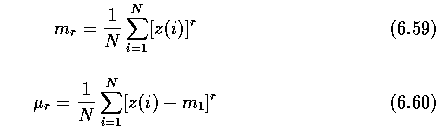
- The r-th normalized contour sequence moment and normalized central contour sequence
moment are defined as
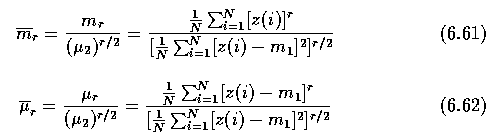
- Less noise-sensitive results can be obtained from the following shape descriptors
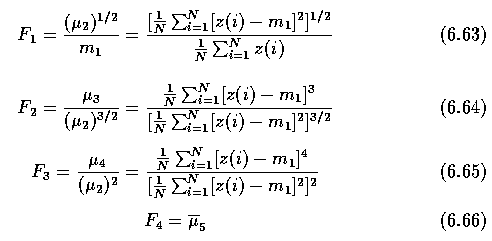
Convex hull
- A region R is convex if and only if for any two points x_1, x_2 from R, the whole line
segment defined by its end-points x_1, x_2 is inside the region R.
- The convex hull of a region is the smallest convex region H which satisfies the
condition R is a subset of H.
- The convex hull has some special properties in digital data which do not exist in the
continuous case. For instance, concave parts can appear and disappear in digital data due
to rotation, and therefore the convex hull is not rotation invariant in digital space.
- The convex hull can be used to describe region shape properties and can be used to build
a tree structure of region concavity.
- A discrete convex hull can be defined by the following algorithm which may also be used
for convex hull construction.
- This algorithm has complexity O(n^2) and is presented here as an intuitive way of
detecting the convex hull.

- More efficient algorithms exist, especially if the object is defined by an ordered
sequence of n vertices representing a polygonal boundary of the object.
- If the polygon P is a simple polygon (self-non-intersecting polygon) which is
always the case in a polygonal representation of object borders, the convex hull may be
found in linear time O(n).
- In the past two decades, many linear-time convex hull detection algorithms have been
published, however more than half of them were later discovered to be incorrect with
counter-examples published.
- The simplest correct convex hull algorithm was developed by Melkman and is now discussed
further.
- Let the polygon for which the convex hull is to be determined be a simple polygon P =
v_1, v_2, ... v_n and let the vertices be processed in this order.
- For any three vertices x,y,z in an ordered sequence, a directional function delta may be
evaluated
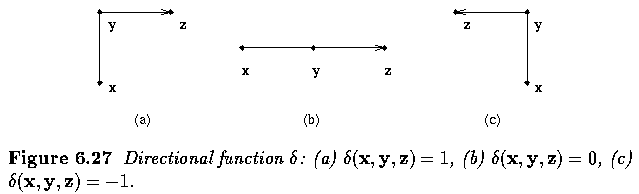
- The main data structure H is a list of vertices (deque) of polygonal vertices already
processed.
- The current contents of H represents the convex hull of the currently processed part of
the polygon, and after the detection is completed, the convex hull is stored in this data
structure.
- Therefore, H always represents a closed polygonal curve, H={d_b, ... ,d_t} where d_b
points to the bottom of the list and d_t points to its top.
- Note that d_b and d_t always refer to the same vertex simultaneously representing the
first and the last vertex of the closed polygon.
- Main ideas of the algorithm:
- The first three vertices A,B,C from the sequence P form a triangle (if not collinear)
and this triangle represents a convex hull of the first three vertices.
- The next vertex D in the sequence is then tested for being located inside or outside the
current convex hull.
- If D is located inside, the current convex hull does not change.
- If D is outside of the current convex hull, it must become a new convex hull vertex and
based on the current convex hull shape, either none, one, or several vertices must be
removed from the current convex hull.
- This process is repeated for all remaining vertices in the sequence P.
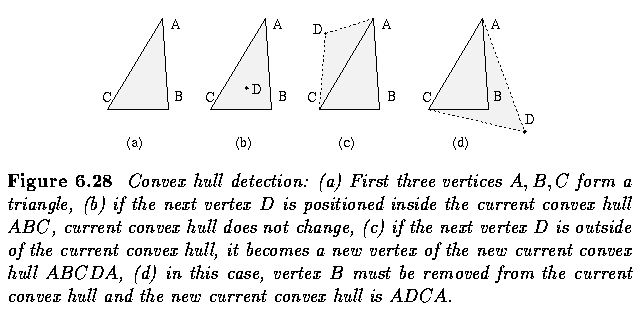
- The variable v refers to the input vertex under consideration, and the following
operations are defined:
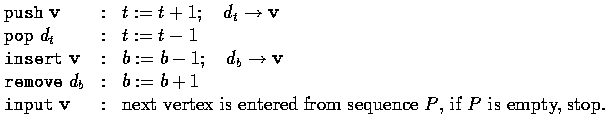

- The algorithm as presented may be difficult to follow, however, a less formal version
would be impossible to implement.
- The following example makes the algorithm more understandable.
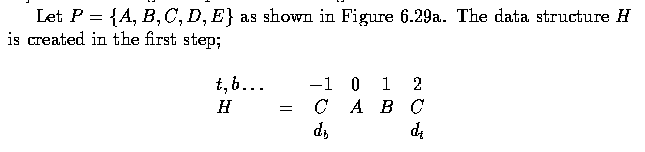
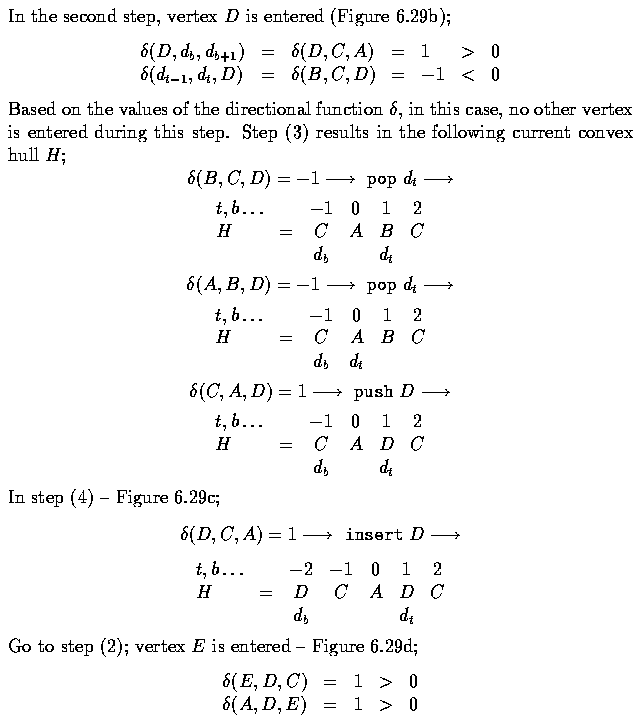
- A new vertex should be entered from P, however there is no unprocessed vertex in the
sequence P and the convex hull generating process stops.
- The resulting convex hull is defined by the sequence H={d_b, ... ,d_t}={D,C,A,D} which
represents a polygon DCAD, always in the clockwise direction.
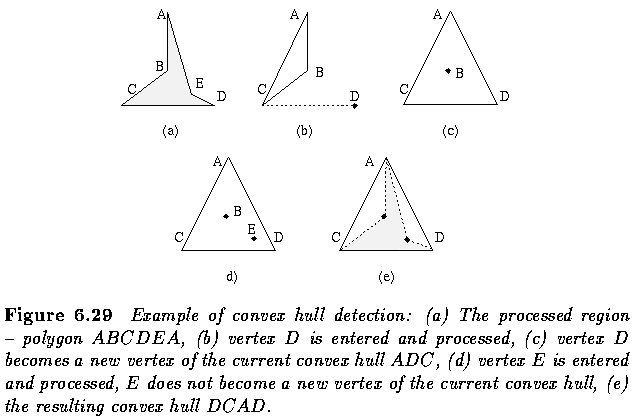
- A region concavity tree is generated recursively during the construction of a
convex hull.
- A convex hull of the whole region is constructed first, and convex hulls of concave
residua are found next.
- The resulting convex hulls of concave residua of the regions from previous steps are
searched until no concave residuum exists.
- The resulting tree is a shape representation of the region.
Graph representation based on region skeleton
- Objects are represented by a planar graph with nodes representing subregions resulting
from region decomposition, and region shape is then described by the graph properties.
- There are two general approaches to acquiring a graph of subregions:
- The first one is region thinning leading to the region skeleton, which can be
described by a graph.
- The second option starts with the region decomposition into subregions, which are
then represented by nodes while arcs represent neighborhood relations of subregions.
- Graphical representation of regions has many advantages; the resulting graphs
- are translation and rotation invariant; position and rotation can be included in the
graph definition
- are insensitive to small changes in shape
- are highly invariant with respect to region magnitude
- generate a representation which is understandable
- can easily be used to obtain the information-bearing features of the graph
- are suitable for syntactic recognition
- Graph representation based on region skeleton
- This method corresponds significantly curving points of a region boundary to graph
nodes.
- The main disadvantage of boundary-based description methods is that geometrically close
points can be far away from one another when the boundary is described - graphical
representation methods overcome this disadvantage.
- The region graph is based on the region skeleton, and the first step is the skeleton
construction.
- There are four basic approaches to skeleton construction:
- thinning - iterative removal of region boundary pixels
- wave propagation from the boundary
- detection of local maxima in the distance-transformed image of the region
- analytical methods
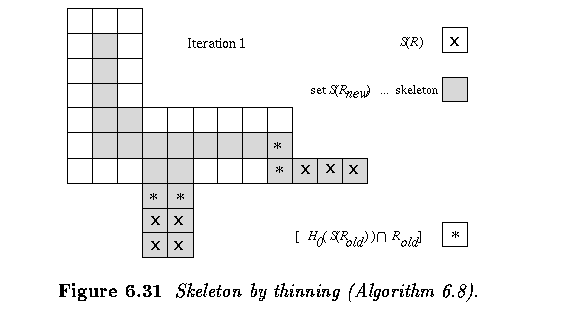
- Most thinning procedures repeatedly remove boundary elements until a pixel set with
maximum thickness of one or two is found. The following algorithm constructs a skeleton of
maximum thickness two.

- Steps of this algorithm are illustrated in the next Figure.
- If there are skeleton segments which have a thickness of two, one extra step can be
added to reduce those to a thickness of one, although care must be taken not to break the
skeleton connectivity.
- Thinning is generally a time-consuming process, although sometimes it is not necessary
to look for a skeleton, and one side of a parallel boundary can be used for skeleton-like
region representation.
- Mathematical morphology is a powerful tool used to find the region skeleton.
- Thinning procedures often use a medial axis transform to construct a region skeleton.
- Under the medial axis definition, the skeleton is the set of all region points which
have the same minimum distance from the region boundary for at least two separate boundary
points.
- Such a skeleton can be constructed using a distance transform which assigns a value to
each region pixel representing its (minimum) distance from the region's boundary.
- The skeleton can be determined as a set of pixels whose distance from the region's
border is locally maximal.
- Every skeleton element can be accompanied by information about its distance from the
boundary -- this gives the potential to reconstruct a region as an envelope curve of
circles with center points at skeleton elements and radii corresponding to the stored
distance values.
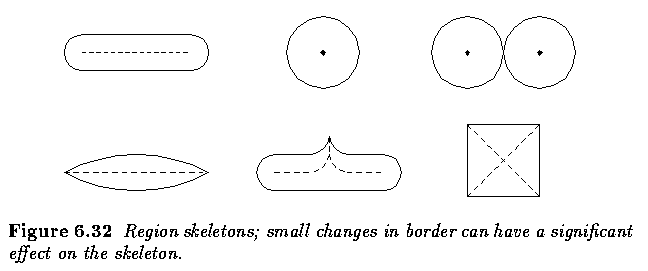
- Small changes in the boundary may cause serious changes in the skeleton.
- This sensitivity can be removed by first representing the region as a polygon, then
constructing the skeleton.
- Boundary noise removal can be absorbed into the polygon construction.
- A multi-resolution approach to skeleton construction may also result in decreased
sensitivity to boundary noise.
- Similarly, the approach using the Marr-Hildreth edge detector with varying smoothing
parameter facilitates scale-based representation of the region's skeleton.
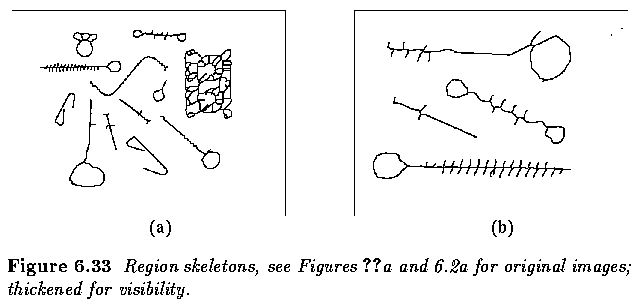
- Skeleton construction algorithms do not result in graphs but the transformation from
skeletons to graphs is relatively straightforward.
- Consider first the medial axis skeleton, and assume that a minimum radius circle has
been drawn from each point of the skeleton which has at least one point common with a
region boundary.
- Let contact be each contiguous subset of the circle which is common to the circle
and to the boundary.
- If a circle drawn from its center A has one contact only, A is a skeleton end-point.
- If the point A has two contacts, it is a normal skeleton point.
- If A has three or more contacts, the point A is a skeleton node-point.

- It can be seen that boundary points of high curvature have the main influence on the
graph.
- They are represented by graph nodes, and therefore influence the graph structure.
- If other than medial axis skeletons are used for graph construction, end-points can be
defined as skeleton points having just one skeleton neighbor, normal-points as having two
skeleton neighbors, and node-points as having at least three skeleton neighbors.
- It is no longer true that node-points are never neighbors and additional conditions must
be used to decide when node-points should be represented as nodes in a graph and when they
should not.
- Region decomposition
- The decomposition approach is based on the idea that shape recognition is a hierarchical
process.
- Shape primitives are defined at the lower level, primitives being the simplest elements
which form the region.
- A graph is constructed at the higher level - nodes result from primitives, arcs describe
the mutual primitive relations.
- Convex sets of pixels are one example of simple shape primitives.
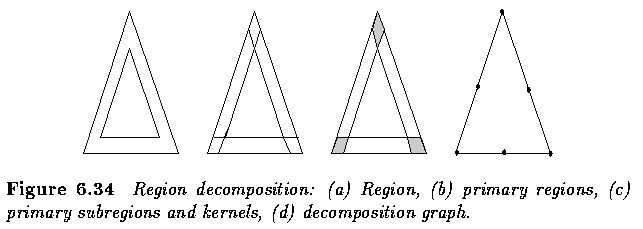
- The solution to the decomposition problem consists of two main steps:
- The first step is to segment a region into simpler subregions (primitives) and the
second is the analysis of primitives.
- Primitives are simple enough to be successfully described using simple scalar shape
properties.
- If subregions are represented by polygons, graph nodes bear the following information;
- Node type representing primary subregion or kernel.
- Number of vertices of the subregion represented by the node.
- Area of the subregion represented by the node.
- Main axis direction of the subregion represented by the node.
- Center of gravity of the subregion represented by the node.
- If a graph is derived using attributes 1-4, the final description is translation
invariant.
- A graph derived from attributes 1-3 is translation and rotation invariant.
- Derivation using the first two attributes results in a description which is size
invariant in addition to possessing translation and rotation invariance.
Region neighborhood graphs
- Any time a region decomposition into subregions or an image decomposition into regions
is available, the region or image can be represented by a region neighborhood graph (the
region adjacency graph being a special case).
- This graph represents every region as a graph node, and nodes of neighboring regions are
connected by edges.
- A region neighborhood graph can be constructed from a quadtree image representation,
from run-length encoded image data, etc.
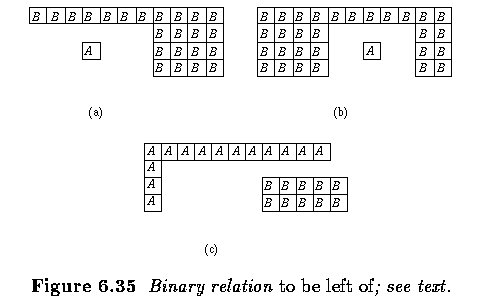
- Very often, the relative position of two regions can be used in the description process
-- for example, a region A may be positioned to the left of a region B, or above
B, or close to B, or a region C may lie between regions A and B, etc.
- We know the meaning of all of the given relations if A,B,C are points, but, with the
exception of the relation to be close, they can become ambiguous if A,B,C are
regions.
- For instance, human observers are generally satisfied with the definition:
- The center of gravity of A must be positioned to the left of the leftmost point of B and
(logical AND) the rightmost pixel of A must be left of the rightmost pixel of B
Last Modified: February 3, 1997
![[Go Back]](../IMAGES/next.gif)

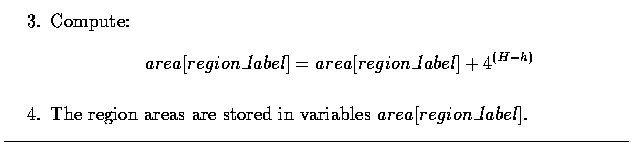

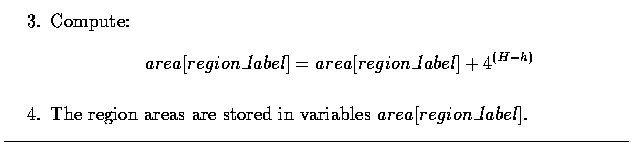
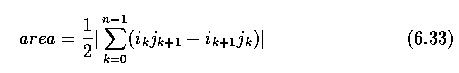


![]()
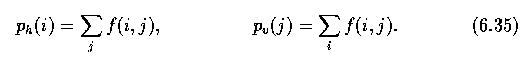


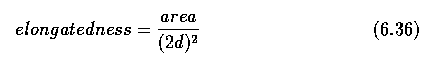
![]()
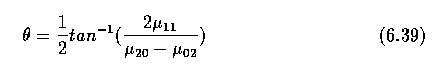


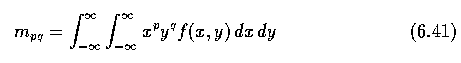
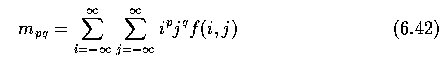
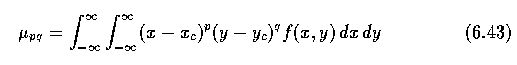
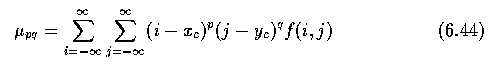

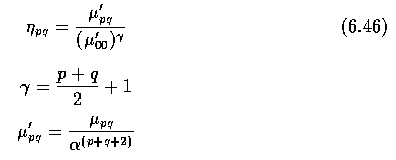

![]()