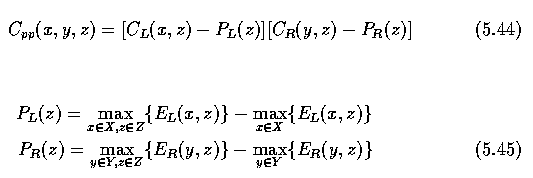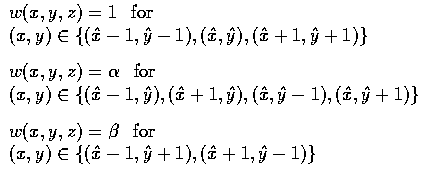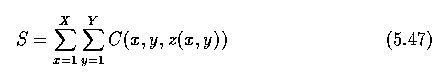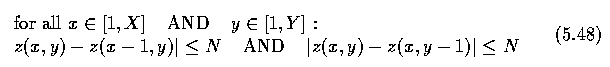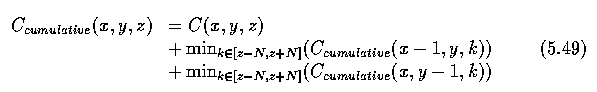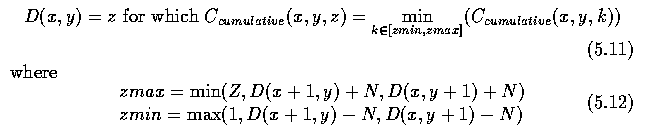55:148 Digital Image Processing
Chapter 5, Part V
Segmentation: Advanced optimal border and surface detection approaches
Related Reading
Sections from Chapter 5 according to the WWW Syllabus.
Chapter 5.5 Overview:
Advanced optimal border and surface detection approaches
- The concept of optimal border detection is extremely powerful and deserves more
attention.
- In the following sections, two advanced graph-based border detection approaches are
introduced.
- The first of them, the Simultaneous detection of border pairs,
facilitates optimal identification of border pairs by finding a path in a
three-dimensional graph.
- The second, the Optimal surface detection method, uses
multi-dimensional graph search for highly efficient determination of surfaces in three- or
higher-dimensional image data.
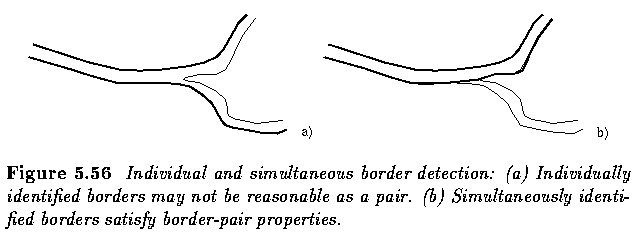
Simultaneous detection of border pairs
- If the goal is to determine borders of elongated objects, it may be advantageous to
search for the pair of left and right borders simultaneously.
- Such an approach facilitates more robust performance if the borders forming the border
pair are interrelated allowing information about one border to help identify the second.
- To search for an optimal border pair, the graph must be three-dimensional.
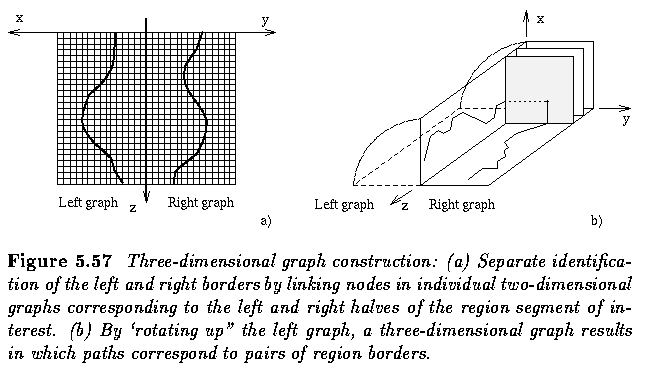
- Each parent node has nine successors corresponding to the possible combinations of
change of positions of the left and right borders with respect to the centerline, thus
forming a 3x3 successor window.
- With this successor rule, all paths through the 3D graph contain one and only one node
from each profile plane in the 3D graph; that is, every path contains a single node
derived from each of the left and right profile lines.
- The cost function for a node in the 3D graph is derived by combining the edge costs
associated with the corresponding pixels on the left and right profiles in a way that
allows the position of the left border to influence the position of the right border and
vice versa.
- Similarly to the 2D case, the cost of a path in the 3D graph is defined as the sum of
the costs of the nodes forming the path.
- The following cost function was found appropriate for description of border properties
of a mutually inter-related border pair. Considering the cost minimization scheme, costs
are assigned to nodes using the following function:
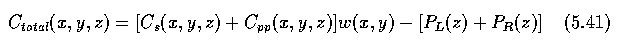
- Where Cs(x,y,z) is the sum of the costs for the left and right borders,
Cpp(x,y,z) is a partial boundary cost, w(x,y) is a weighting function, and
PL(z) and PR(z) are partial
boundary costs.
- The edge costs of the left and right edge candidates located at positions x and y on
profile z are inversely related to effective edge strength or other appropriate local
border property descriptor E_L(x,z), E_R(y,z):
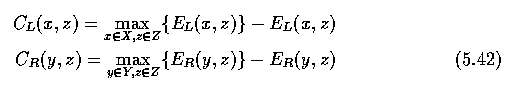
- X and Y are sets of integers ranging from 1 to the length of the left and right halves
of the region profiles, and Z is the set of integers ranging from 1 to the length of the
region centerline.
- To help avoid detection of regions adjacent to the region of interest, knowledge about
the probable direction of the actual border may be incorporated into the local edge
property descriptors E_L(x,z), E_R(y,z).
- Considering the individual terms of the cost function, the term C_s is the sum of the
costs for the left and right border candidates and causes the detected borders to follow
image positions with low cost values. It is given by:
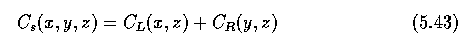
- The C_pp term is useful in cases where one border has higher contrast (or other stronger
border evidence) than the opposite border and causes the position of the low contrast
border to be influenced by the position of the high contrast border. It is given by:
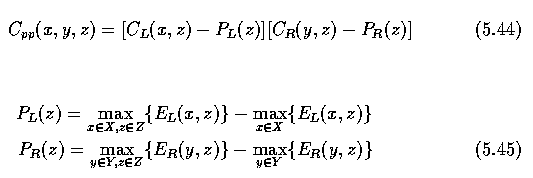
- The w(x,y,z) component of the cost function incorporates a model of the region boundary
in a way that causes the positions of the left and right borders to follow certain
preferred directions relative to the model.
- This component has the effect of discriminating against borders that are unlikely to
correspond to the actual region borders when considered as a pair. This is accomplished by
including a weighting factor that depends on the direction by which a node is reached from
its predecessor.
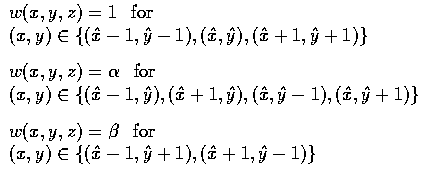
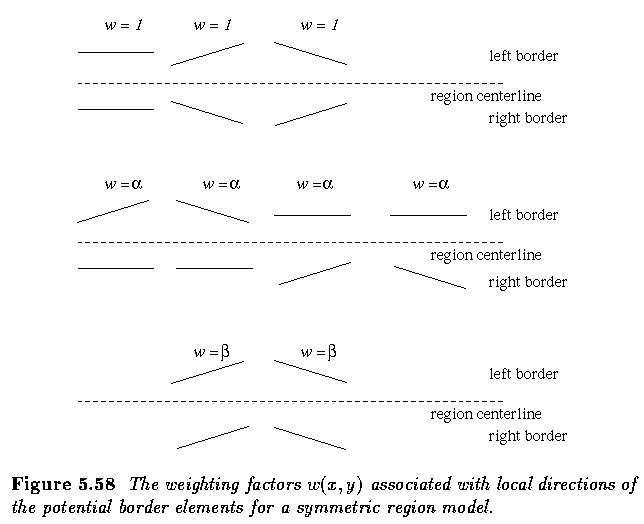
- The influence of the region model is determined by the values of alpha and
beta, typically alpha > beta.
- The larger the values of alpha and beta, the stronger is the model's influence
on the detected borders.
- Typical values of alpha range from 1.2 to 1.8 and beta from 1.4 to 2.2.
- As the number of possible paths in a 3D graph is very large, the identification of the
optimal path can be very computationally demanding.
- For example, for a 3D graph with xyz nodes, where z is the length in pixels of the
region centerline, the number of possible paths is approximately 9^z.
- With conventional border detection, the number of possible paths in the two
two-dimensional graphs of the same size is about 3^z.
- Improving the graph search performance is of great importance, and the P_L(z)+P_R(z)
term in the cost function represents the lower bound heuristic, and does not influence the
detected border; it does, however, substantially improve search efficiency if a heuristic
graph searching approach is used.
- A second way to increase search efficiency - a multi-resolution approach.
- To enhance border detection accuracy, a multi-stage border identification process may
also be included. The goal of the first stage is to identify reliably the approximate
borders of the region segment of interest while avoiding detection of other structures.
Having identified the approximate border positions, the second stage is designed to
localize the actual region borders accurately.
- In the first stage, a relatively strong region model is used. Region boundaries
identified in the low-resolution image are used in the second stage to guide the search
for the optimal borders in the full-resolution cost image, as described in the previous
paragraph. A somewhat weaker region model may be used in the second stage to allow more
influence from the image data
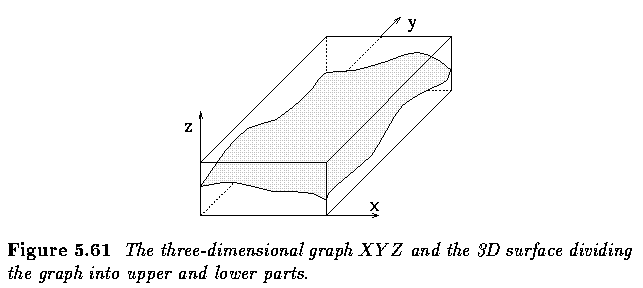
Optimal surface detection
- If three-dimensional volumetric data are available, the task may be to identify
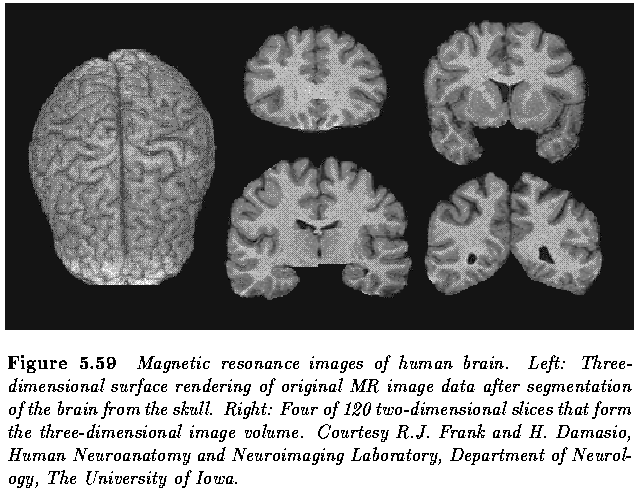
three-dimensional surfaces representing object boundaries in the three-dimensional space.
- Example: brain cortex visualization from three-dimensional magnetic resonance (MR) data
sets of a human brain
- Consider a 3D graph that corresponds in size with the 3D image data volume; the graph
nodes correspond to image voxels.
- The legality of the surface is defined by the 3D surface connectivity requirements that
depend on the application at hand, and the total cost associated with a surface can be
calculated as the sum of individual costs of all nodes forming the surface.
- It should be possible to determine the optimal surface by application of optimal graph
searching principles similar to those presented earlier. Unfortunately, standard graph
searching approaches cannot be directly extended from a search for a path to a search for
a surface.
- The search for an optimal surface results in combinatorial explosion of the task's
complexity, and the absence of an efficient searching algorithm has until recently
represented a limiting factor on 3D surface detection.
- An approach to optimal surface detection based on cost minimization in a graph was
developed by Thedens and Fleagle that used standard graph searching principles applied to
a transformed graph. While the method guaranteed surface optimality, it was impractical
due to its enormous computational requirements.
- Frank and Dove developed a new approach to direct surfaces detection that is based on
dynamic programming and avoids the problem of combinatorial explosion by introducing local
conditions that must be satisfied by all legal surfaces.
- The approach can be generalized to searching higher-dimensional spaces
- The cost S of a surface is defined as
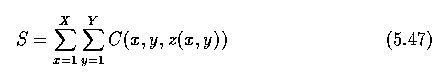
- The connectivity constraint guarantees surface continuity in 3D. The parameter N
represents the maximum allowed change in the z-co-ordinate of the surface along the unit
distance in x and y directions. If N is small, the legal surface is stiff and the
stiffness decreases with larger values of N.
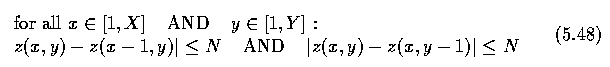
- Each internal node of the graph may have 4(2N+1) legal neighbors that have to be
examined when constructing the 3D graph.
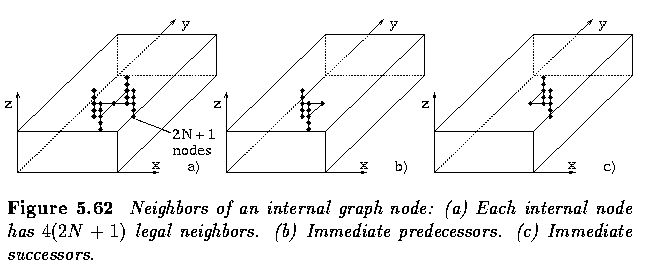
- The graph is searched starting from the vertical column with co-ordinates (1,1,z) in z
-- x -- y co-ordinate order towards the column (X,Y,z).
- The cumulative surface cost is defined as the sum of the local cost associated with the
node (x,y,z) and the sum of the two cost minima identified in the two columns constructed
in the 3D graph that represent the immediate predecessors.
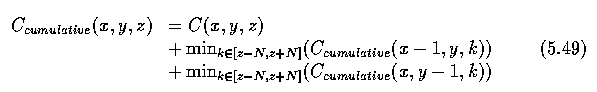
- The surface construction proceeds in the reversed z-y-x order.
- Propagation of the connectivity constraint guarantees the legality of the resulting
surface. The z-coordinate of the surface-node in the (x,y) column, denoted by D(x,y) is
defined as
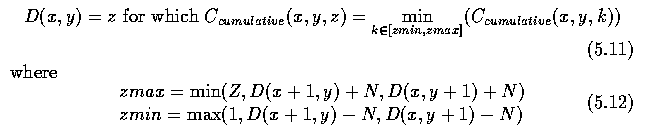
- The backtracking process continues until the optimal node in the column (1,1,z) is
identified.


- Assuming a circular surface, the 3D graph can be constructed by unfolding the circular
structure, considering the additional set of links from the set of graph columns (X,y,z)
to the columns (1,y,z) to close the surface, and applying the graph-searching algorithm.
- However, the first and last row of optimal nodes may not satisfy the surface
connectivity constraints. While it is possible to consider this constraint in the graph
construction, a substantial increase in computational complexity results.
- There is a practical solution to the problem based on selecting a new cut-set of nodes
along the y-co-ordinate to unfold the circular graph. Although not theoretically
guaranteeing success under all circumstances, this approach has demonstrated practical
applicability.
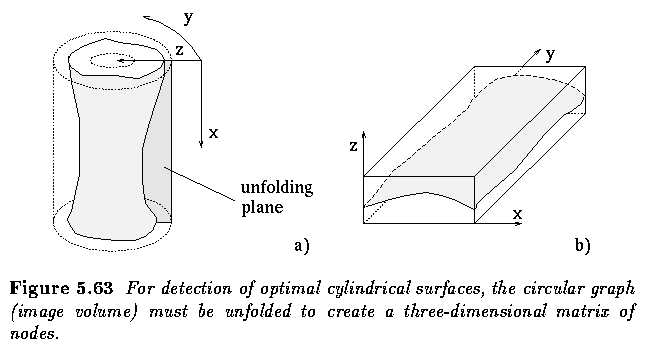
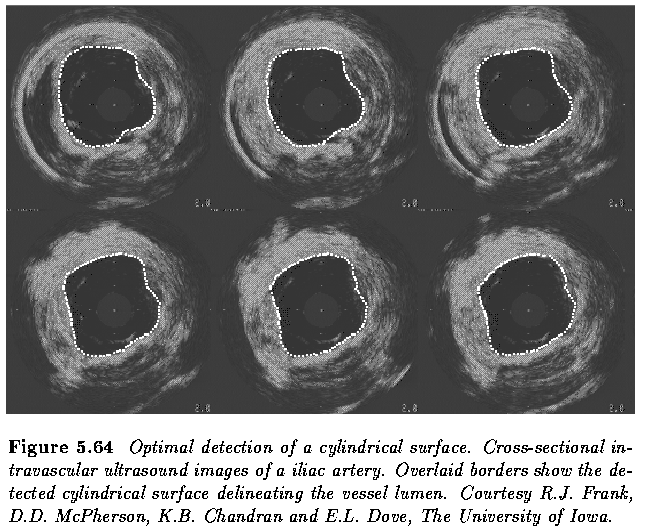
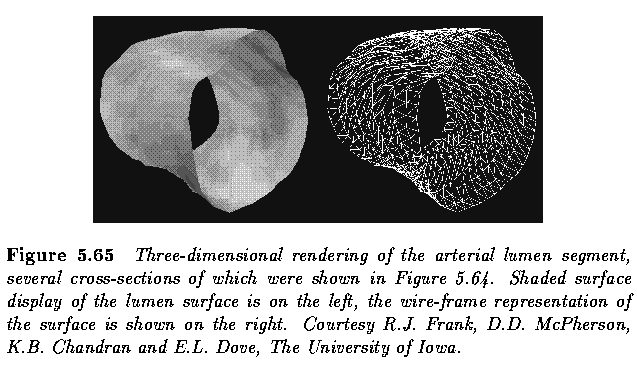
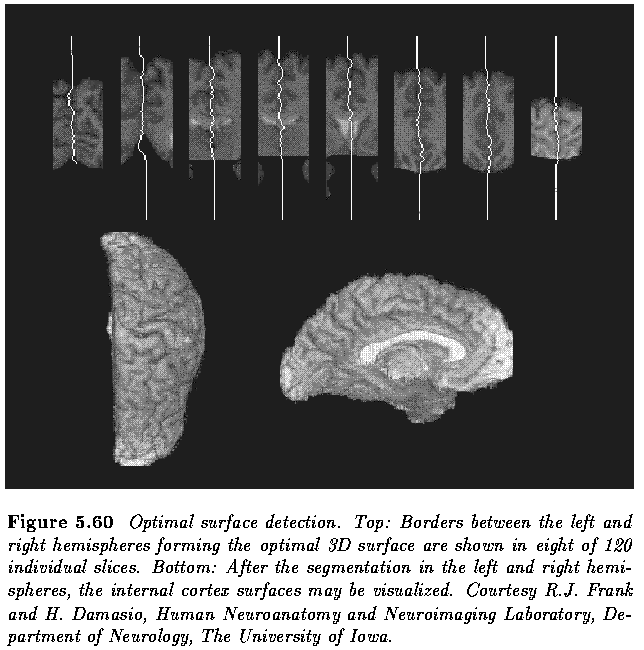
- In the brain segmentation example above, the cost function was based on inverted gray
level values of the image voxels after the ventricles were three-dimensionally filled not
to represent a large low-cost region.
- In the IVUS data, the cost function was based on inverted edge strength and edge
direction.
- The size of the graphs ranged from 100 x 25 x 10 for the intravascular ultrasound image
sequences to 256 x 120 x 40 for the MR brain images.
Last Modified: January 27, 1997
![[Go Back]](../IMAGES/next.gif)



![]()
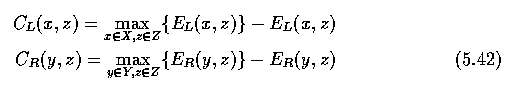
![]()