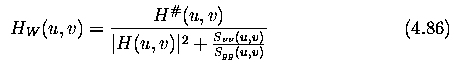55:148 Digital Image Processing
Chapter 4, Part IV
Image Pre-processing: Image restoration
Related Reading
Sections from Chapter 4 according to the WWW Syllabus.
Chapter 4.4 Overview:
Image restoration
- Image restoration - suppressing image degradation using knowledge about its
nature
Image restoration as inverse
convolution of the whole image
- Most image restoration methods are based on convolution applied globally to the whole
image.
- Degradation causes:
- defects of optical lenses,
- nonlinearity of the electro-optical sensor,
- graininess of the film material,
- relative motion between an object and camera
- wrong focus,
- atmospheric turbulence in remote sensing or astronomy,
- etc.
- The objective of image restoration is to reconstruct the original image from its
degraded version.
- Image restoration techniques - two groups:
- Deterministic methods - applicable to images with little noise and a known
degradation function.
- The original image is obtained from the degraded one by a transformation inverse to the
degradation.
- Stochastic techniques - the best restoration is sought according to some
stochastic criterion, e.g., a least squares method.
- In some cases the degradation transformation must be estimated first.
- It is advantageous to know the degradation function explicitly.
- The better this knowledge is, the better are the results of the restoration.
- There are three typical degradations with a simple function:
- Relative constant speed movement of the object with respect to the camera,
- wrong lens focus,
- and atmospheric turbulence.
- In most practical cases, there is insufficient knowledge about the degradation, and it
must be estimated and modeled.
- Methods:
- A priori knowledge about degradation - either known in advance or obtained before
restoration.
- If it is clear in advance that the image was degraded by relative motion of an object
with respect to the sensor then the modeling only determines the speed and direction of
the motion.
- An example of parameters obtained before restoration is an attempt to estimate
parameters of a capturing device such as a TV camera or digitizer.
- A posteriori knowledge is obtained by analyzing the degraded image.
- A typical example is to find some interest points in the image (e.g. corners, straight
lines) and guess how they looked before degradation.
- Another possibility is to use spectral characteristics of the regions in the image that
are relatively homogeneous.
- A degraded image g can arise from the original image f by a process which can be
expressed as
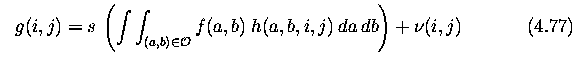
where s is some nonlinear function and nu describes the noise.
- The degradation is very often simplified by
- neglecting the nonlinearity
- assuming that the function h is invariant with respect to position in the image.
- Degradation can be then expressed as convolution
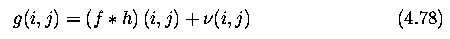
- If the degradation is given by equation (4.78) and the noise is not significant then
image restoration equates to inverse convolution (also called deconvolution).
- If noise is not negligible then the inverse convolution is solved as an overdetermined
system of linear equations.
Degradations that are easy to restore
- Some degradations can be easily expressed mathematically (convolution) and also restored
simply in images.
- The Fourier transform H of the convolution function is used.
Relative motion of the camera and object
- Assume an image is acquired with a camera with a mechanical shutter.
- Relative motion of the camera and the photographed object during the shutter open time T
causes smoothing of the object in the image.
- Suppose V is the constant speed in the direction of the x axis; the Fourier transform
H(u,v) of the degradation caused in time T is given by
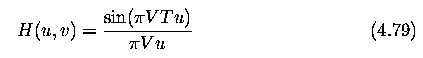
Wrong lens focus
- Image smoothing caused by imperfect focus of a thin lens can be described by the
following function

where J_1 is the Bessel function of the first order, r^2 = u^2 + v^2, and a is the
displacement.
Atmospheric turbulence
- needs to be restored in remote sensing and astronomy
- caused by temperature non-homogeneity in the atmosphere that deviates passing light
rays.
- The mathematical model
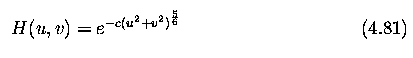
where c is a constant that depends on the type of turbulence which is usually found
experimentally.
The power 5/6 is sometimes replaced by 1.
Practical Experiment 4.K - VIP Version
- From VIP, open restore_working_test.vip
- Modify the workspace so that it first distorts the original image by horizontal
camera motion distortion.
- Although not exactly corresponding to Eq. 4.79, horizontal camera motion distortion
can be modeled using a simple sinusoidal filter - create a sinusoidal image of the same
size as your input image ( the node for generating a sinusoidal image can be found here as sinusoid.nod ) and create a
sinusoidal filter . Use this filter instead of the Low pass filter that was used before.
- By changing the numbers of waves along width and height, you can create a
"double exposure" image that may have resulted from an abrupt camera motion.
- there are 7 parameters you may adjust in the sinusoid node - they are accesible
at the bottom of the Properties box
- width: the width of the filter
- height: the height of the filter
- wnum: the number of sinusoids along the width
- hnum: the number of sinusoids along the height
- wp: the phase offset along the width
- hp: the phase offset along the height
- amplitude: the amplitude of the sinusoid
- Restore the image by application of an inverse filter.
- Experiment with the motion distortion parameters.
Practical Experiment 4.K - Khoros Version
- From cantata, open the restore-working-test.wksp.
- Modify the workspace so that it first distorts the original image by horizontal
camera motion distortion.
- Although not exactly corresponding to Eq. 4.79, horizontal camera motion distortion
can be modeled using a simple sinusoidal filter - create a sinusoidal image of the same
size as your input image (Input/output-> Generate Data -> Sinusoid) and create a
sinusoidal filter . Use this filter instead of the Low pass filter that was used before.
- By changing the numbers of waves along width and height, you can create a
"double exposure" image that may have resulted from an abrupt camera motion.
- Restore the image by application of an inverse filter.
- Experiment with the motion distortion parameters.
Inverse filtration
- based on the assumption that degradation was caused by a linear function h(i,j)
- the additive noise nu is another source of degradation.
- It is further assumed that nu is independent of the signal.
- Applying the Fourier transform to equation (4.78)
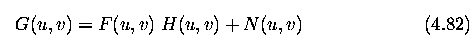
- The degradation can be eliminated if the restoration filter has a transfer function that
is inverse to the degradation h ... or in Fourier transform H^-1(u,v).
- The undegraded image F is derived from its degraded version G.
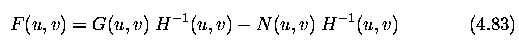
- This equation shows that inverse filtration works well for images that are not corrupted
by noise.
- If noise is present and additive error occurs, its influence is significant for
frequencies where H(u,v) has small magnitude. These usually correspond to high frequencies
u,v and thus fine details are blurred in the image.
- The changing level of noise may cause problems as well because small magnitudes of
H(u,v) can cause large changes in the result.
- Inverse filter values should not be of zero value so as to avoid zero divides in
equation (4.83).
Practical Experiment 4.L - VIP Version
- Save the images to_restore2.kdf
and inverse-filter2.kdf to your
diphome directory
- These are Khoros images, however VIP is able to read them with the Read_Binary node
in the project.
- It is necessary to use the binary Khoros form of the images due to their complex
nature ( this may be seen by displaying the image in a Live_Image node before the
TypeConvert node. If you examine the pixel intensities, you will notice that they
are complex values.
- Save restore.vip to your diphome
directory.
- From VIP, open restore.vip.
- Display the input image ( to_restore2.kdf
) - you will see it's degradation.
- What kind of image degradation is it?
- Obtain its Fourier transform, apply the precomputed inverse filter
(inverse-filter2.kdf) , perform the inverse Fourier transform and display the result.
Practical Experiment 4.L - Khoros Version
- From cantata, open the restore.wksp.
- Display the input image - you will see it's degradation.
- What kind of image degradation is it?
- Obtain its Fourier transform, apply the precomputed inverse filter , perform the
inverse Fourier transform and display the result.
Practical Experiment 4.M - VIP Version
- From VIP, open restore-working-test.vip
- Follow the processing flow - generation of the distortion filter and its application
to restore the image using inverse filtering.
Practical Experiment 4.M - Khoros Version
- From cantata, open the restore-working-test.wksp.
- Follow the processing flow - generation of the distortion filter and its application
to restore the image using inverse filtering.
Wiener filtration
- It is no surprise that inverse filtration gives poor results in pixels suffering from
noise since the noise is not taken into account.
- Wiener filtration explores a priori knowledge about the noise.
- Restoration by the Wiener filter gives an estimate of the original uncorrupted image f
with minimal mean square error e^2
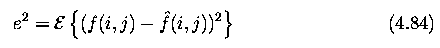
- No constraints applied to equation (4.84)
- optimal estimate ^f is the conditional mean value of the ideal image f under the
condition g
- complicated from the computational point of view
- also, the conditional probability density between the optimal image f and the corrupted
image g is not usually known.
- the optimal estimate is in general a nonlinear function of the image g.
- Minimization of equation (4.84) is easy if estimate ^f is a linear combination of the
values in the image g -close-optimal solution
- H_W ... Fourier transform of the Wiener filter - considers noise - see Eq. (4.86) below
- G ... Fourier transform of the degraded image
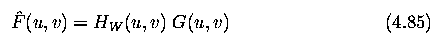
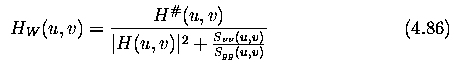
where H is the transform function of the degradation
# denotes complex conjugate
S_{nu nu} is the spectral density of the noise
S_{gg} is the spectral density of the degraded image |
- If Wiener filtration is used, the nature of degradation H and statistical parameters of
the noise need to be known.
- Wiener filtration theory solves the problem of a posteriori linear mean square estimate
-- all statistics (e.g., power spectrum) should be available in advance.
- Note that the inverse filter discussed earlier is a special case of the Wiener filter
where noise is absent i.e. S_{nu nu} = 0.
Last Modified: October 1,1996
![[Go Back]](../IMAGES/next.gif)
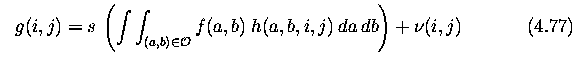
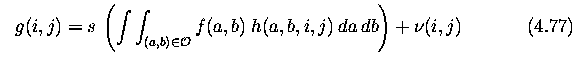
![]()
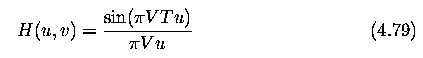

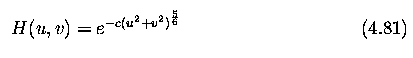
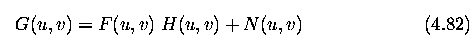
![]()
![]()
![]()