| NOTE: This page is posted to the web in order to share results with the swept volume community. The material below introduces the basic theory and demonstrates a simple example of sweeping using the Jacobian rank deficiency condition. |
Please forward any feedback to Prof. K. Abdel-Malek
![]()
Formulation
Before getting involved in the mathematical formulation, we shall first demonstrate the need for such mathematics through a simple example. Consider the planar sweep of a circle along an axis. The circle is defined by the equation
![]() (1)
(1)
The axis along which the circle will be sweeping (or in this case can be called extruding) is also defined by an equation
![]() (2)
(2)
where this axis shall start at the origin ![]() and extending to
and extending to ![]() . Therefore, the
parameter
. Therefore, the
parameter ![]() varies
as
varies
as ![]() as shown in
Fig. 2.1.
as shown in
Fig. 2.1.
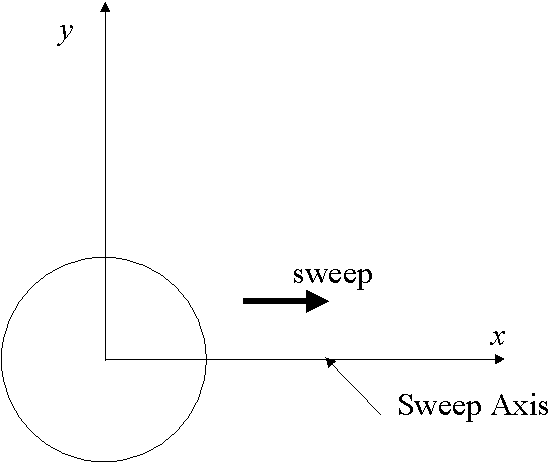
Fig. 2.1
To understand the sweep concept and especially when dealing with multiple parameter sweeps, it is helpful to think of a point P on the swept entity (the circle) moving along the circle at all times. This point traces the circle for each round it makes. Sweeping of this circle while this point is moving along an axis yields a trace covering the swept area illustrated in Fig. 2.2(a). The swept area consists of all points touched (swept) by P.
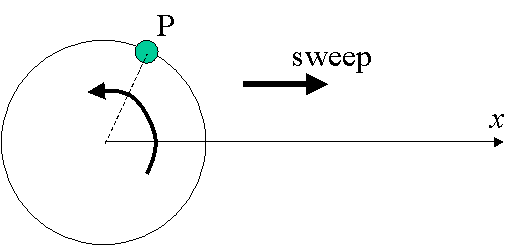
Fig. 2.2a A geometric entity is represented by a point circulating along its trajectory
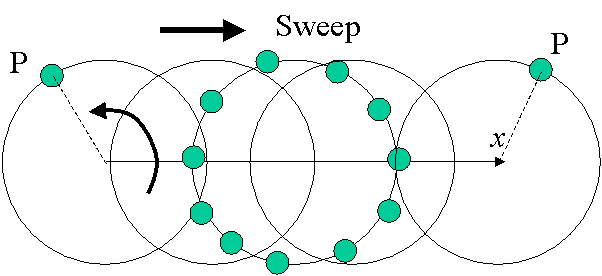
Fig. 2.2b Sweeping of a planar entity
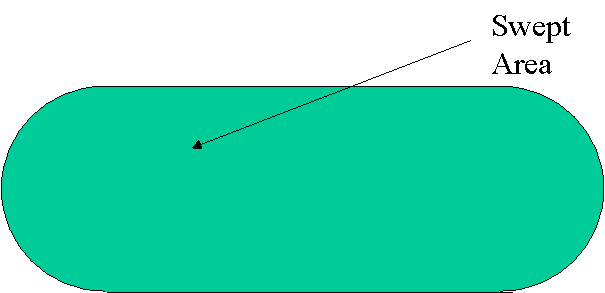
Fig. 2.2c Resulting swept area
The task at hand here is to identify the boundary to this
swept area. At the beginning of this sweep, the original circle
is clearly identified part of which is the boundary as shown in
Fig. 2.3. At the end of the sweep, i.e., at ![]() , a circle is also
identified and a segment of which is also on the boundary.
, a circle is also
identified and a segment of which is also on the boundary.
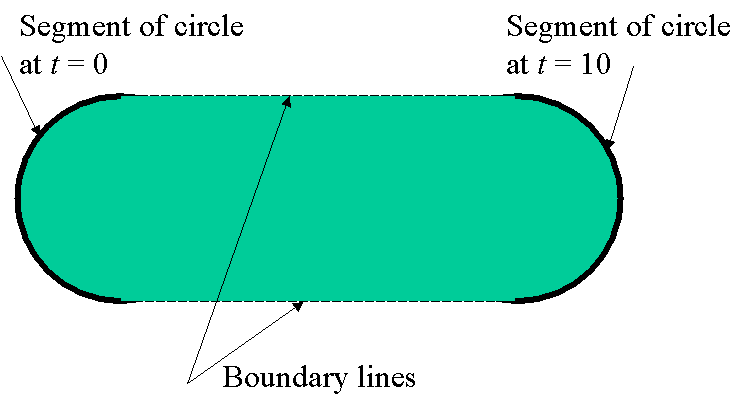
Fig. 2.3 Boundaries to the swept area
In order to find these boundaries and without presenting any complicated proofs, we shall present a simple mathematical formulation for delineating the boundary.
The totality of the swept area of the sweep described above is characterized by
![]() (3)
(3)
![]() (4)
(4)
There are two types of borders to be identified.
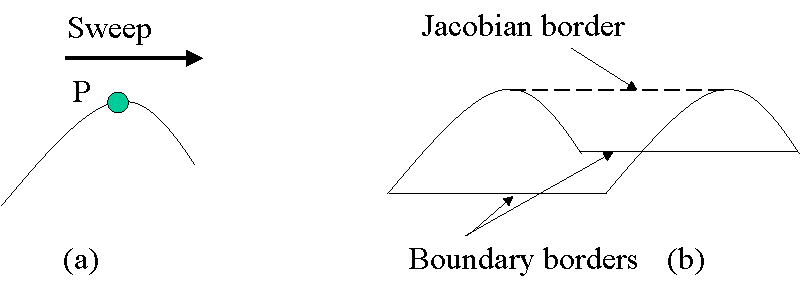
Fig. 2.4 (a) A curve with its maximum at P (b) Sweeping and identifying borders
Returning to our simple example, we shall first compute the
Jacobian of ![]() . The
Jacobian is
. The
Jacobian is
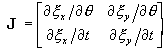 (5)
(5)
![]()
Similar to finding the maximum point in a function by setting its derivative to zero, the determinant of the sweep Jacobian is set to zero such that
![]() (6)
(6)
which identifies two solutions for ![]() and for
and for ![]() . Substituting these solutions into
. Substituting these solutions into ![]() yields the other two
boundaries as
yields the other two
boundaries as
![]()
![]()
which are the two lines closing the boundary to the swept area shown dotted in Fig. 2.3. Now that all boundary curves have been determined, the swept area can be identified by a function given by Eq. () and its boundary curves as shown in Fig. 2.5.
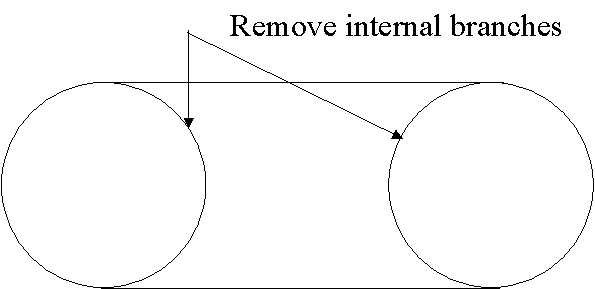
Fig. 2.5 Removing internal branches
It is interesting to see if this concept works if the circle is to be swept along the y-axis.
For this case, the circle is still defined by Eq. (), and the y-axis (sweep axis) is given by
![]() (7)
(7)
The sweep function is then
![]() (8)
(8)
and the sweep Jacobian is
![]() (9)
(9)
The determinant of the Jacobian set to zero is
![]() (10)
(10)
Solving this equation yields two points on the circle at ![]() and
and ![]() as shown in Fig. 2.6.
as shown in Fig. 2.6.
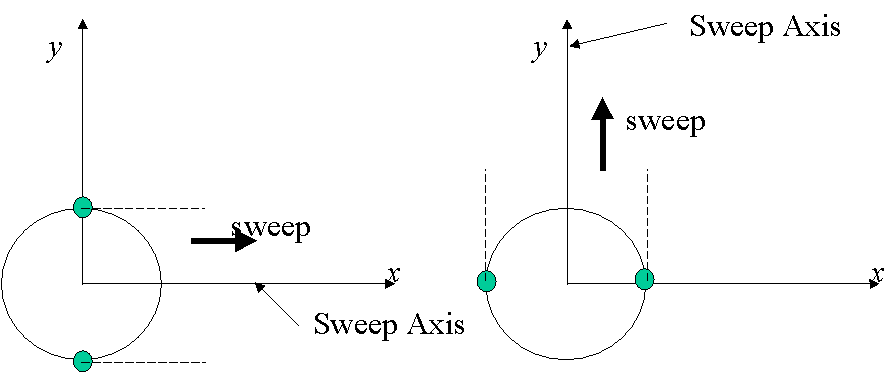
Fig. 2.6 (a) Sweep along the x-axis (b) along the y-axis
The method for characterizing the swept volume and its boundary, illustrated above in rather general terms, will be presented in the next section in a rigorous mathematical formulation.
Formulation
Consider a geometric entity parametrized in terms of one or
more variables as a ![]() vector given by
vector given by ![]() , where
, where ![]() , i.e., the geometric entity can be a curve, a
surface, or an entity in a higher dimensional space. In order to
generalize the formulation, we shall also consider a boundary
imposed on
, i.e., the geometric entity can be a curve, a
surface, or an entity in a higher dimensional space. In order to
generalize the formulation, we shall also consider a boundary
imposed on ![]() in the
form of constraints on the parameters
in the
form of constraints on the parameters ![]() characterized by inequality constraints
in the form of
characterized by inequality constraints
in the form of
![]() (11)
(11)
Consider a second geometric entity parametrized in terms of
one or more variables as a ![]() vector
vector ![]() , where
, where ![]() , where also this entity can be a curve, a surface,
or a volume. This entity also has a defined boundary
characterized by
, where also this entity can be a curve, a surface,
or a volume. This entity also has a defined boundary
characterized by
![]() (12)
(12)
The accessible set generated by the sweep of ![]() on
on ![]() can be defined as (the
term swept volume is reserved to indicate the actual volume of
the set)
can be defined as (the
term swept volume is reserved to indicate the actual volume of
the set)
![]() (13)
(13)
where q is the extended vector defined by
![]() (14)
(14)
and ![]() is the
is the ![]() rotation matrix
defining the orientation of the swept entity. In fact,
rotation matrix
defining the orientation of the swept entity. In fact, ![]() characterizes the set
of all points on the surface and on the boundary of the swept
volume. The aim of this section is to determine the boundary to
this set.
characterizes the set
of all points on the surface and on the boundary of the swept
volume. The aim of this section is to determine the boundary to
this set.
Consider the derivative of the accessible set (Equation 3) with respect to time
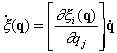 (15)
(15)
where the dot denotes a derivative with respect to time and the matrix
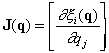 (16)
(16)
is called the Jacobian of the sweep and has dimension ![]() . The left-hand side of
Equation 5 is the velocity
. The left-hand side of
Equation 5 is the velocity ![]() of a point moving in the swept volume having a
parameter velocity vector
of a point moving in the swept volume having a
parameter velocity vector ![]() .
.
Square Jacobian-No Limits
In the case of a square Jacobian, the determination of singular values is directly obtained. The determinant of a square Jacobian is equated to zero and solved for its roots.
Example of a Three-Parameter Square Jacobian
To demonstrate the formulation for sweeps that do not have limits in their definitions, consider the sweeping of the entity generated above (swept area) along an axis to give it an extrusion height.
Let the swept entity be given by Eq. () as
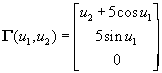 (17)
(17)
that is to be swept on the entity
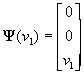 (18)
(18)
with an orientation specified by the rotation matrix
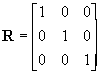 (19)
(19)
where ![]() and
and ![]() . The function
characterizing this sweep is given by
. The function
characterizing this sweep is given by
![]() (20)
(20)
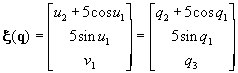 (21)
(21)
where ![]() . The
sweep Jacobian is computed as
. The
sweep Jacobian is computed as
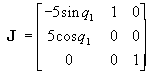 (22)
(22)
Since this is a square Jacobian, the determinant is evaluated and equated to zero as
![]() (23)
(23)
Solving for the roots yields ![]() and
and ![]() . These are the singular sets due to the Jacobian. We
shall denote these sets by
. These are the singular sets due to the Jacobian. We
shall denote these sets by ![]() such that
such that ![]() and
and ![]() .
Other singularities are due to the limits imposed on
.
Other singularities are due to the limits imposed on ![]() and
and ![]() such that
such that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Substituting each singular set into the sweep function ![]() yields the equations
of the hyperentities. For example, substituting
yields the equations
of the hyperentities. For example, substituting ![]() yields
yields
![]() (24)
(24)
Similarly, substituting ![]() yields the hyperentity
yields the hyperentity
![]() (25)
(25)
both shown in Fig. 2.7.
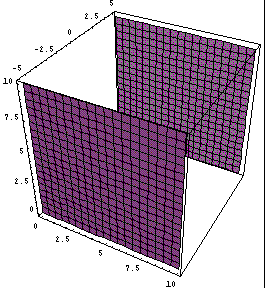
Fig. 2.7 (a) Hypersurfaces ![]() and
and ![]()
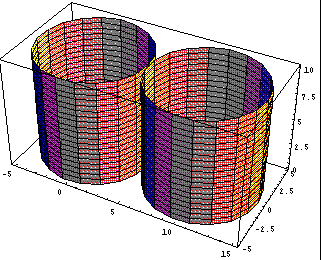
Fig. 2.7 (b) Hypersurfaces ![]() and
and ![]()
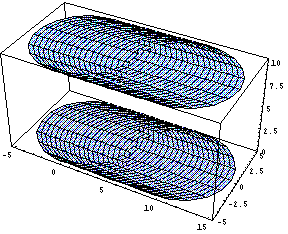
Fig. 2.7 (c) Hypersurfaces ![]() and
and ![]()
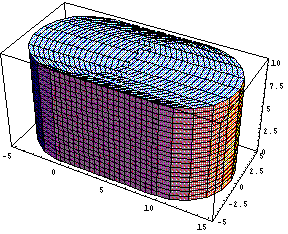
Fig. 2.8 Swept volume